
分析 (1)先代入特殊角的三角函数值,然后化简求值;
(2)先化简括号内的分式,然后化除法为乘法进行化简,最后代入求值.
解答 解:(1)2sin30°-tan45°-$\sqrt{{{(1-tan{{60}°})}^2}}$,
=2×$\frac{1}{2}$-1-$\sqrt{(1-\sqrt{3})^{2}}$,
=1-1-|1-$\sqrt{3}$|,
=1-$\sqrt{3}$;
(2)($\frac{x+3}{x+2}$-$\frac{x-1}{x}$)÷$\frac{x+1}{{{x^2}+4x+4}}$,
=$\frac{{x}^{2}+3x-{x}^{2}-x+2}{x(x+2)}$×$\frac{(x+2)^{2}}{x+1}$,
=$\frac{2(x+1)}{x(x+2)}$×$\frac{(x+2)^{2}}{x+1}$,
=$\frac{2(x+2)}{x}$.
把x=$\sqrt{2}$代入上式,得
原式=$\frac{2(\sqrt{2}+2)}{\sqrt{2}}$=2+2$\sqrt{2}$.
点评 本题考查了实数的运算,特殊角的三角函数值以及分式的化简求值,属于基础题,熟记实数混合运算法则即可解题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
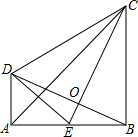 如图,CB⊥AB,垂足为B,DA⊥AB,垂足为A,E为AB的中点,AB=BC,CE⊥BD.
如图,CB⊥AB,垂足为B,DA⊥AB,垂足为A,E为AB的中点,AB=BC,CE⊥BD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
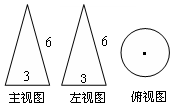 一个几何体的三视图如图,其中主视图都是腰长为6、底边长为3的等腰三角形,则这个几何体的侧面展开图的面积为( )
一个几何体的三视图如图,其中主视图都是腰长为6、底边长为3的等腰三角形,则这个几何体的侧面展开图的面积为( )| A. | 3π | B. | 18π | C. | 8π | D. | 9π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB∥CD∥EF,则下列各式中正确的是( )
如图,AB∥CD∥EF,则下列各式中正确的是( )| A. | ∠1+∠2+∠3=180° | B. | ∠1+∠2-∠3=90° | C. | ∠1-∠2+∠3=90° | D. | ∠2+∠3-∠1=180° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com