
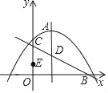
【题目】如图,二次函数y=ax2+bx+c的图象与x轴的一个交点坐标![]() ,顶点A的坐标为
,顶点A的坐标为![]() .直线
.直线![]() 交x轴于点B,交y轴于点C,与抛物线的对称轴交于点D,E为y轴上的一个动点.
交x轴于点B,交y轴于点C,与抛物线的对称轴交于点D,E为y轴上的一个动点.
(1)求这条抛物线的解析式和点D的坐标;
(2)若以C、D、E为顶点的三角形与△ACD相似,求点E的坐标;
(3)若点E关于直线BC的对称点M恰好落在抛物线上,求点M的坐标.
【答案】(1)这条抛物线的解析式为:y=![]() ,点D的坐标为:(2,2).(2)E点坐标为(0,1)或(0,
,点D的坐标为:(2,2).(2)E点坐标为(0,1)或(0,![]() ).(3)M点坐标为(2,
).(3)M点坐标为(2,![]() )或(﹣1,
)或(﹣1,![]() ).
).
【解析】
(1)将函数解析式写成顶点式,代入顶点及抛物线与x轴交点坐标可以求得解析式;点D横坐标即为顶点横坐标,代入直线解析式即可求得点D纵坐标,从而可得结论;
(2)设点E坐标为(0,m),用含m的代数式表示出CE,利用相似三角形的性质列比例式可解;
(3)从点E关于直线BC的对称点M向y轴作垂直,由∠MEH与∠OBC相等,利用三角函数求得相关线段的长度,从而用一个未知数表示出点M的坐标,再将其代入抛物线解析式可求得这个未知数,从而得解.
(1)∵二次函数y=ax2+bx+c的图象与x轴的一个交点坐标(2+3![]() ,0),顶点A的坐标为(2,
,0),顶点A的坐标为(2,![]() ),
),
设其顶点式解析式为y=a(x﹣2)2+![]() ,把(2+3
,把(2+3![]() ,0)代入可得:a=﹣
,0)代入可得:a=﹣![]() ,
,
∴y=﹣![]() (x﹣2)2+
(x﹣2)2+![]() ,即y=
,即y=![]() ,
,
∵直线![]() 与抛物线的对称轴交于点D,当x=2时,y=2
与抛物线的对称轴交于点D,当x=2时,y=2
∴点D坐标为(2,2).
∴这条抛物线的解析式为:y=![]() ,点D的坐标为:(2,2).
,点D的坐标为:(2,2).
(2)设点E坐标为(0,m)
∵直线![]() 交x轴于点B,交y轴于点C,当x=0时,y=3;当y=0时,x=6,
交x轴于点B,交y轴于点C,当x=0时,y=3;当y=0时,x=6,
∴点C坐标为(0,3),点B坐标为(6,0),
∴CD=![]() ,AD=
,AD=![]() ,CE=3﹣m,
,CE=3﹣m,
①当△ADC∽△DCE时,![]() ,即
,即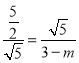 ,解得m=1;
,解得m=1;
②当△ADC∽△ECD时,![]() ,即
,即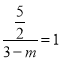 ,解得m=
,解得m=![]() ,
,
∴E点坐标为(0,1)或(0,![]() ).
).
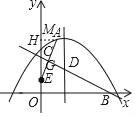
(3)如图,作MH⊥y轴于点H,设ME与BC交于点G,MH=m,则∠MEH=∠OBC
∴tan∠OBC=tan∠MEH=![]() ,
,
∴HE=2m,EM=![]() m
m
在Rt△CEG中,EG=![]() EM=
EM=![]() ,
,
∴CG=![]() m ,CE=
m ,CE=![]() m ,
m ,
∴OE=OC﹣CE=3﹣![]() m ,
m ,
∴OH=OE+EH=3﹣![]() m+2m=3+
m+2m=3+![]() m,
m,
∴点M坐标为(m,3+![]() m),
m),
把M(m,3+![]() m)代入y=﹣
m)代入y=﹣![]() (x﹣2)2+
(x﹣2)2+![]() 得:m1=2,m2=﹣1,
得:m1=2,m2=﹣1,
∴M点坐标为(2,![]() )或(﹣1,
)或(﹣1,![]()
![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题
打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元,比不打折少花费多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次数学兴趣小组活动中,对一个数学问题做如下探究:
(问题背景)
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC、BC、CD之间的数量关系.小明同学探究此问题的思路是:将△BCD绕点D逆时针旋转90°到△AED处,点B、C分别落在点A、E处(如图②),易证点C、A、E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.
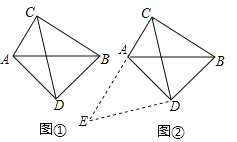
(简单应用)
(1)在图①中,若AC=![]() ,BC=2
,BC=2![]() ,则CD= .
,则CD= .
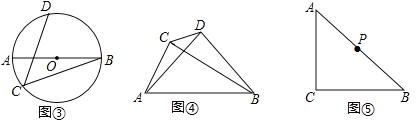
(2)如图③,AB是⊙O的直径,点C、D在⊙O上,![]() ,若AB=10,BC=8,求CD的长.
,若AB=10,BC=8,求CD的长.
(拓展延伸)
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=a,BC=b(a<b),求CD的长.(用含a,b的代数式表示).
(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=![]() AC,CE=CA,点Q为AE的中点,请直接写出线段PQ与AC的数量关系.
AC,CE=CA,点Q为AE的中点,请直接写出线段PQ与AC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘巡逻艇航行至海面B处时,得知正北方向上距B处20海里的C处有一渔船发生故障,就立即指挥港口A处的救援艇前往C处营救.已知C处位于A处的北偏东45°的方向上,港口A位于B的北偏西30°的方向上.求A、C之间的距离.(结果精确到0.1海里,参考数据![]() )( )
)( )
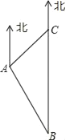
A. 7.3海里B. 10.3海里C. 17.3海里D. 27.3海里
查看答案和解析>>
科目:初中数学 来源: 题型:
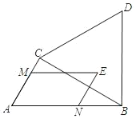
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=4,△BCD为等边三角形,点E为△BCD围成的区域(包括各边)内的一点,过点E作EM∥AB,交直线AC于点M,作EN∥AC,交直线AB于点N,则![]() AN+AM的最大值为_____.
AN+AM的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
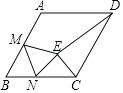
【题目】在菱形ABCD中,∠B=60°,BC=2cm,M为AB的中点,N为BC上一动点(不与点B重合),将△BMN沿直线MN折叠,使点B落在点E处,连接DE,CE,当△CDE为等腰三角形时,线段BN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
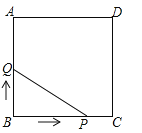
【题目】(3分)如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.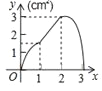 B.
B.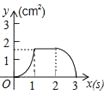 C.
C.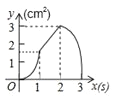 D.
D.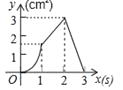
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第 24 届冬奥会将于 2022 年在北京和张家口举行,冬奥会的项目有滑雪(如跳台滑雪、高山滑雪、单板滑雪等)、滑冰(如短道速滑、速度滑冰、花样滑冰等)、冰球、冰壶等.如图,有 5 张形状、大小、质地均相同的卡片,正面分别印有高山滑雪、速度滑冰、冰球、单板滑雪、冰壶五种不同的图案,背面完全相同.现将这 5 张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是滑雪项目图案的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com