
���� ��1�����Ƚ�ԭʽ����Ϊa+2-b+��b-4��$\sqrt{2}$=0��Ȼ������a��b�������������a��b��ֵ��Ȼ�����������ľ��빫ʽ����õ�C�������ꣻ
��2������A��AC��x�ᣬ��OB���C����BD��AC������ΪD������õ�C�����꣬Ȼ�������AC�ij���������ݡ�AOB�����Ϊ9�з�������⼴�ɣ�
��3����AF��x�ᣬBE��x�ᣮ����ABC���������AOD������ı�ֵ��ת��ΪAB��AD�ı�ֵ��Ȼ������ƽ���߷��߶γɱ��������ɵõ�AB��AD=FE��OF=1��1���ʴ˿ɵõ�����Ĵ𰸣�
��� �⣺��1����a+2+$\sqrt{2}$b=4$\sqrt{2}$+b��
��a+2-b+��b-4��$\sqrt{2}$=0��
��a��b����������
��$\left\{\begin{array}{l}{b=4}\\{a+2=b}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{a=2}\\{b=4}\end{array}\right.$
��A��m-2��2����B��m+2��4����
���C��������Ϊa�����������ľ��빫ʽ�ɵõ���$\frac{a+0}{2}$=$\frac{2+4}{2}$����ã�a=6��
���C��������Ϊ6��
��2����ͼ1��ʾ������A��AC��x�ᣬ��BD��AC������ΪD��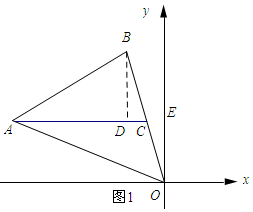
��AC��x�ᣬ
���C��������Ϊ2��
��ֱ��BC�Ľ���ʽΪy=kx������B���������ã���m+2��k=4�����k=$\frac{4}{m+2}$��
��ֱ��OB�Ľ���ʽΪy=$\frac{4}{m+2}$x��
��y=2����ã�$\frac{4}{m+2}$x=2����ã�x=$\frac{m+1}{2}$��
��C��$\frac{m+1}{2}$��2����
��AC=$\frac{m+1}{2}$-��m-2��=$\frac{6-m}{2}$��
�ߡ�AOB�����Ϊ9��
��$\frac{1}{2}$��4��|$\frac{6-m}{2}$|=9�����m=-3��m=15��
��3���Ƕ�ֵ��
��ͼ2��ʾ����AF��x�ᣬBE��x�ᣮ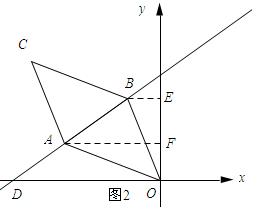
���ı���OACBΪƽ���ı��Σ�
���ABC�����=��ABO�������
���ABC���������AOD�����=��ABO���������AOD�����=AB��AD��
��BE��AF��OD��
��AB��AD=FE��OF=1��1��
���ABC���������AOD�����=1��1��
���� ������Ҫ��������ı��ε��ۺ�Ӧ�ã��������ҪӦ����ƽ���ı��ε����ʡ�ƽ���߷��߶γɱ��������������ε������ʽ������ϵ�����������������Ľ���ʽ�����ձ���ĸ����ߵ������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ֪��y1=x+m��x�ᡢy��ֱ��ڵ�A��B����˫����y2=$\frac{k}{x}$��x��0���ֱ��ڵ�C��-1��2����D��a��1����
��ͼ����ֱ֪��y1=x+m��x�ᡢy��ֱ��ڵ�A��B����˫����y2=$\frac{k}{x}$��x��0���ֱ��ڵ�C��-1��2����D��a��1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
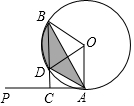 ��ͼ����֪PAΪ��O�����ߣ�AΪ�е㣬BΪ��O��һ�㣬��AOB=120�㣬����B��BC��PA�ڵ�C��BC����O�ڵ�D������AB��AD��
��ͼ����֪PAΪ��O�����ߣ�AΪ�е㣬BΪ��O��һ�㣬��AOB=120�㣬����B��BC��PA�ڵ�C��BC����O�ڵ�D������AB��AD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com