
【题目】(1)观察推理:如图 1,△ABC 中,∠ACB=90°,AC=BC,直线 L 过点C,点 A,B 在直线 L 同侧,BD⊥L, AE⊥L,垂足分别为D,E
求证:△AEC≌△CDB
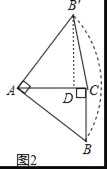
(2)类比探究:如图 2,Rt△ABC 中,∠ACB=90°,AC=4,将斜边 AB 绕点 A 逆时针旋转 90°至 AB’, 连接B’C,求△AB’C 的面积
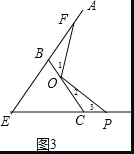
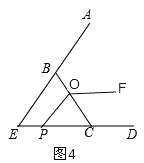
(3)拓展提升:如图 3,等边△EBC 中,EC=BC=3cm,点 O 在 BC 上且 OC=2cm,动点 P 从点 E 沿射线EC 以 1cm/s 速度运动,连接 OP,将线段 OP 绕点O 逆时针旋转 120°得到线段 OF,设点 P 运动的时间为t 秒。
当t= 秒时,OF∥ED


若要使点F 恰好落在射线EB 上,求点P 运动的时间t
【答案】(1)证明见解析;(2)8;(3)①1;②4s.
【解析】
(1)先利用等角的余角相等得到![]() ,则可根据“AAS”证明
,则可根据“AAS”证明![]() ;
;
(2)作B′D⊥AC于D,如图2,先证明△B′AD≌△ABD得到B′D=AC=4,然后根据三角形面积公式计算;
(3)因为OF∥ED,所以∠POF+∠OPC=180°,因为∠POF=120°,所以∠OPC=60°,因为△BEC是等边三角形,所以∠BCE=60°=∠OPC,∠E=∠OPC=60°,△COP是等边三角形,PC=OC,即可求解;如图3,利用旋转的性质得![]() ,OP=OF,再证明
,OP=OF,再证明![]() 得到PC=OB=1,则BP=BC+PC=4,然后计算点P运动的时间t.
得到PC=OB=1,则BP=BC+PC=4,然后计算点P运动的时间t.
(1)如图1,
∵BD⊥l,AE⊥l,
∴∠AEC=∠BDC=90°,
∵∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,
∴∠EAC=∠BCD,
在△AEC和△CDB中
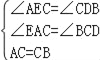
∴△AEC≌△CDB;
(2)作B′D⊥AC于D,如图2,
∵斜边AB绕点A逆时针旋转90°至AB′,
∴AB′=AB,∠B′AB=90°,
即∠B′AC+∠BAC=90°,
而∠B+∠CAB=90°,
∴∠B=∠B′AC,
在△B′AD和△ABD中
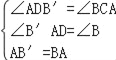 ,
,
∴△B′AD≌△ABD,
∴B′D=AC=4,
∴△AB′C的面积=![]() ×4×4=8;
×4×4=8;
(3)①由题意得:EP=t,则PC=3﹣t,
如图4,∵OF∥ED
∴∠POF+∠OPC=180°,
∵∠POF=120°,
∴∠OPC=60°,
∵△BEC是等边三角形,
∴∠BCE=60°=∠OPC,
∴∠E=∠OPC=60°,
∴△COP是等边三角形,
∴PC=OC=2,
∴2=3﹣t,
∴t=1,
即当t=1秒时,OF∥ED,
故答案为:1;
②如图3,∵OC=2,
∴OB=BC﹣OC=1,
∵线段OP绕点O逆时针旋转120°得到线段OF,
∴∠FOP=120°,OP=OF,
∴∠1+∠2=60°,
∵△BCE为等边三角形,
∴∠BCE=∠CBE=60°,
∴∠FBO=120°,∠PCO=120°,
∴∠2+∠3=∠BCE=60°,
∴∠1=∠3,
在△BOF和△CPO,
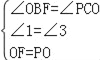 ,
,
∴△BOF≌△CPO,
∴PC=OB=1,
∴BP=BC+PC=3+1=4,
∴点P运动的时间t=![]() =4s.
=4s.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】已知∠BOC=60°,OF平分∠BOC.若AO⊥BO,OE平分∠AOC,则∠EOF的度数是( )
A. 45°
B. 15°
C. 30°或60°
D. 45°或15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.

(1,1),(3,1),(1,3),(1,1);
(-1,3),(-1,5),(-3,3),(-1,3);
(-5,1),(-3,-1),(-3,1),(-5,1);
(-1,-1),(1,-1),(-1,-3),(-1,-1).
(1)观察所得的图形,你觉得它像什么?
(2)求出这四个图形的面积和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.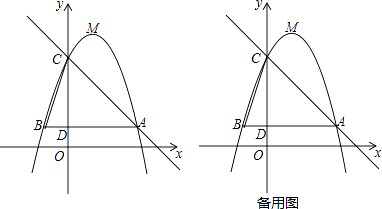
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,在四边形 ABCD 中,AB∥DC,E 是 BC 中点,若 AE 是∠BAD 的平分线,试探究 AB,AD,DC 之间的数量关系,请直接写出结论,无需证明.
(2)如图 2,在四边形ABCD 中,AB∥DC,AF 与DC 的延长线交于点F,E 是BC 中点,若AE 是∠BAF 的平分线,试探究AB,AF,CF 之间的数量关系,证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
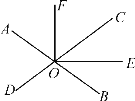
【题目】如图,直线AB,CD相交于点O,OE是∠COB的平分线,∠FOE=90°,若∠AOD=70°.
(1)求∠BOE的度数;
(2)OF是∠AOC的平分线吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形ABCD中,F是CD边上一点(不和C,D重合),过点D做DG⊥BF交BF延长线于点G.连接AG,交BD于点E,连接EF,交CD于点M.若DG=6,AG=7 ![]() ,则EF的长为 .
,则EF的长为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com