
����Ŀ��2019��ȫ����Сѧ������ȫ�����ա������ǡ��䰮��������ȫ�����С���С���ﵥ����ѧ����������һ�Σ�����Ҫ��ij���飬�������ۻص��վ������»���꣬��������ȥѧУ.���������������õ�ʱ����·�̵Ĺ�ϵʾ��ͼ������ͼ���ṩ����Ϣ�ش��������⣺
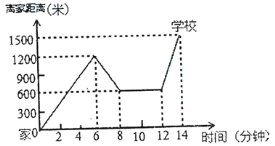
��1��С���ҵ�ѧУ��·����________�ף�С�������ͣ����________���ӣ�
��2��������ѧ;�У�С��ȫ��һ������________���ӣ�һ��������________��.
��3��������Ϊ�ﵥ�����ٶȳ���300��/�־ͳ����˰�ȫ�ȣ���������ѧ��;���ĸ�ʱ���С���ﳵ�ٶ���죿�ٶ��ڰ�ȫ���������С����һ������������.
���𰸡���1��1500�� 4����2��14��2700��3����12���ӵ�14����С���ﳵ�ٶ���죬�ٶȲ��ڰ�ȫ���ڣ���������������.
��������
��1����ͼ��֪��(14,1500)��֪С���ҵ�ѧУ��·����1500�ף��ɣ�8��600���ͣ�12��600��С�������ͣ����12-8=4���ӣ�
��2���ɣ�14��1500����֪С��ȫ��һ������14���ӣ�һ����ʻ��·�̰�����;�ۻص�·�̣����㼴�ɵ�;
��3�������ٶȹ�ʽ�����Էֱ���㣺�ۻ�֮ǰ���ٶȡ��ۻ����ʱ���ٶȡ�����굽ѧУ���ٶȣ������ȽϿ�֪����������ѧ��;�� ��12���ӵ�14����С���ﳵ�ٶ���죬�����ٶ��� 450 ��/�֣����ۻ����ʱ���ٶȡ�����굽ѧУ���ٶȶ������ٶ��ڰ�ȫ����,����ȫ.���Ľ��飺Ӧ�ú��������ٶ���300��/�����ڣ���֤��ȫ.
�⣺��1����ͼ��֪��С���ҵ�ѧУ��·����1500�ף�С�������ͣ����12-8=4���ӣ�
��2��С��ȫ��һ������14���ӣ�
һ����ʻ�ˣ�1200+��1200-600��+��1500-600��=2700���ף�
��3���ۻ�֮ǰ���ٶ�=1200��6=200����/�֣�
�ۻ����ʱ���ٶ�=��1200-600����2=300����/�֣���
����굽ѧУ���ٶ�=��1500-600����2=450����/�֣�
�����ȽϿ�֪��С���ڴ���굽ѧУ��ʱ���ٶ���죮
������������ѧ��;�� ��12���ӵ�14����С���ﳵ�ٶ���죬�����ٶ��� 450 ��/�֣�
���ۻ����ʱ���ٶȡ�����굽ѧУ���ٶȶ������ٶ��ڰ�ȫ����,����ȫ�����Ľ��飺Ӧ�ú��������ٶ���300��/�����ڣ���֤��ȫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�����ӳ�25�ף�б����һ��ǽ�ϣ����ӵ���ǽ7�ס�

��1��������ӵĶ���������ж�ߣ�
��2��������ӵĶ����»���4�ף���ô���ӵĵ���ˮƽ�����˼��ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ���ڷ���ʱ��������·������ͼ��1������ʾ��
���ڷ���ʱ��������·������ͼ��1������ʾ��![]() ����������ߣ�
����������ߣ�![]() ����������ߣ��������
����������ߣ��������![]() ������һ����ֱ�ھ���
������һ����ֱ�ھ���![]() ������
������![]() �������ߣ�
�������ߣ�![]() ��
��![]() �ļн�
�ļн�![]() ������ǣ�
������ǣ�![]() ��
��![]() �ļн�
�ļн�![]() �з����.���ݿ�ѧʵ��ɵã�
�з����.���ݿ�ѧʵ��ɵã�![]() .��ͼ��1����
.��ͼ��1����![]() ��
��![]() ��������ϵ�ǣ�____________���ɣ�___________��
��������ϵ�ǣ�____________���ɣ�___________��

![]() ���������ǿ����������������������ཻ��ƽ�澵���в��.��ͼ��2����һ����������
���������ǿ����������������������ཻ��ƽ�澵���в��.��ͼ��2����һ����������![]() ���뵽ƽ�澵
���뵽ƽ�澵![]() �ϡ���
�ϡ���![]() ���䵽ƽ�澵
���䵽ƽ�澵![]() �ϣ��ֱ�ƽ�澵
�ϣ��ֱ�ƽ�澵![]() �����õ��������
�����õ��������![]() .
.

��1�����������![]() �����������
�����������![]() �ķ������ȥ����
�ķ������ȥ����![]() ����
����![]() ����
����![]() ______
______![]() ��
��![]() ______
______![]() ��
��
��2�����룺��![]() ______
______![]() ʱ���κ��䵽ƽ�澵
ʱ���κ��䵽ƽ�澵![]() �ϵĹ���
�ϵĹ���![]() ����ƽ�澵
����ƽ�澵![]() ��
��![]() ���������������
�����η�����������![]() �뷴�����
�뷴�����![]() ����ƽ�е�.���������ѧ����֪ʶ����֪˵��.
����ƽ�е�.���������ѧ����֪ʶ����֪˵��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�س���Ʒѷ�����ͼ��x��km����ʾ��ʻ��̣�y��Ԫ����ʾ���ѣ������ͼ�����������⣺
��1���õس�������� Ԫ��
��2����x��2ʱ����y��x֮��ĺ�����ϵʽ��
��3����ij�˿���һ�γ˳�������Ϊ18km������λ�˿��踶������Ѷ���Ԫ��
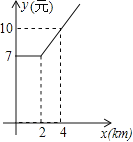
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��֪����ͼ����D�ǡ�ABC�ı�AB���е㣬�ı���BCED��ƽ���ı��Σ�
��1����֤���ı���ADCE��ƽ���ı��Σ�
��2���ڡ�ABC�У���AC��BC�����ı���ADCE���� ������ֻд���ۣ�����֤����
��3���ڣ�2���������£���AC��BCʱ����֤���ı���ADCE�������Σ�
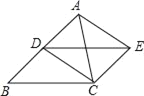
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=mx+n��m��0����ͼ���뷴��������y=![]() ��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����ΪM��BM=OM��OB=2
��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����ΪM��BM=OM��OB=2![]() ����A��������Ϊ4��
����A��������Ϊ4��
��1����÷�����������һ�κ����Ľ���ʽ��
��2������MC�����ı���MBOC�������
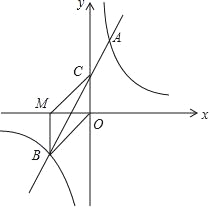
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ���������ʦ�е���ѧ����ĩ���Եĵ�17��������ľ����������������е�ijһ�˶�������ľ����������Ҫ15Сʱ������Ҫ10Сʱ������Ҫ8Сʱ��
��1������ס��ҡ�������ͬʱ�ľ�����ô��Ҫ����ʱ����ɣ�
��2��������ռס��ҡ������ס��ҡ����������Ĵ��������ľ���ÿһ����ÿ�˸��ľ�1Сʱ����ôҪ����Сʱ��ɣ�
��3���ܷ�ѣ�2������˵�ļס��ҡ����Ĵ������ʵ�����������IJ��䣬ʹ��������������ʱ��������ǰ��Сʱ��������Ҫ������Ϊ���ܣ���Ҫ˵�����ɣ�����Ϊ�ܣ�������˵��һ�������Ĵ��������Ӧ����ǰ����ʱ������ľ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��)ͼ������һ���ֹܻ�����ϵ�˹��ţ��ŵĹ���ACB����Ϊ�����ߵ�һ����(��ͼ��)������(��Ϊˮƽ��)�빰���ô�ֱ�������ϵ�����ӣ���ù���
�Ŀ��ABΪ200�ף���AB�е�O���20�״���һ�߶�Ϊ48��ϵ�ˣ�
��1�������м�ϵ��OC�ij��ȣ�
��2��������ϵ��֮��ļ���Ϊ5��(������ϵ�˵Ĵ�ϸ)�����Ƿ����һ��ϵ�˵ij���ǡ����OC���ȵ�һ�룿��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+3��ͼ�����A����1��0������������Ϊ��1��m����
��1����ö��κ����Ĺ�ϵʽ��mֵ��
��2�����ͼ����������⣺��ֱ��д���𰸣�
����xȡʲôֵʱ���ú�����ͼ����x���·���
������1��x��2ʱ��ֱ��д������y��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com