
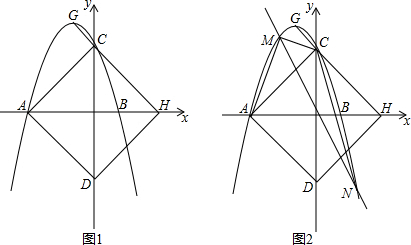
���� ��1�����ݶ��κ���y=ax2+bx+3��ͼ����x���ཻ�ڵ�A��-3��0����B��1��0����Ӧ�ô���ϵ���������a��b��ֵ������������κ����ı���ʽ��
��2�����ȷֱ������C��G��H��D�����ꣻȻ���жϳ�AO=CO=DO=HO=3��AH��CD���жϳ��ı���ACHD�������μ��ɣ�
��3������ME��x���ڵ�E����MF��y���ڵ�F�������ı���ADCM�����ΪS���ɵ�S=S�ı���AOCM+S��AOD���ٷֱ����S�ı���AOCM��S��AOD���ɣ�
���������N�������ǣ�t1��p1������NI=|t1|������S��CMN=S��COM+S��CON=$\frac{3}{2}$��|t|+|t1|�����ٸ���t��0��t1��0���ɵ�S��CMN=$\frac{3}{2}$��|t|+|t1|��=$\frac{3}{2}{��t}_{1}-t��$=$\frac{21}{4}$���ݴ����t1-t=$\frac{7}{2}$��Ȼ�����k1��k2��ֵ�Ƕ��٣��������t1��t2��ֵ�Ƕ��٣��ٰ����Ǵ���S����t�ĺ�������ʽ�����S��ֵ�Ƕ��ټ��ɣ�
��� �⣺��1���߶��κ���y=ax2+bx+3��ͼ����x���ཻ�ڵ�A��-3��0����B��1��0����
��$\left\{\begin{array}{l}{9a-3b+3=0}\\{a+b+3=0}\end{array}\right.$
���$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$
����κ����ı���ʽΪy=-x2-2x+3��
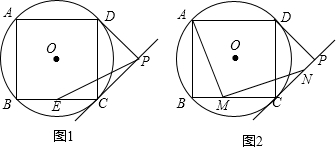
��2����ͼ1��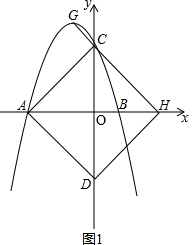 ��
��
�߶��κ����ı���ʽΪy=-x2-2x+3��
���C��������0��3����
��y=-x2-2x+3=-��x+1��2+4��
���G�������ǣ�-1��4����
�ߵ�C������Ϊ��0��3����
����CG���ڵ�ֱ�ߵĽ���ʽ��y=mx+3��
��-m+3=4��
��m=-1��
��CG���ڵ�ֱ�ߵĽ���ʽ��y=-x+3��
���H�������ǣ�3��0����
���D�������ǣ�0��p����
��$\frac{p-0}{0-��-3��}=\frac{3-0}{0-3}=-1$��
��p=-3��
��AO=CO=DO=HO=3��AH��CD��
���ı���ACHD�������Σ�
��3������ͼ2����ME��x���ڵ�E����MF��y���ڵ�F��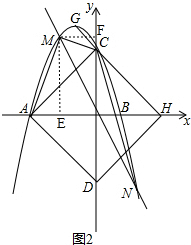 ��
��
���ı���ADCM�����ΪS��
��S=S�ı���AOCM+S��AOD��
��AO=OD=3��
��S��AOD=3��3��2=4.5��
�ߵ�M��t��p����y=kx��y=-x2-2x+3�ڵڶ������ڵĽ��㣬
���M�������ǣ�t��-t2-2t+3����
��ME=-t2-2t+3��MF=-t��
��S�ı���AOCM=$\frac{1}{2}$��3����-t2-2t+3��$+\frac{1}{2}��3����-t��$=-$\frac{3}{2}$t2-$\frac{9}{2}$t+$\frac{9}{2}$��
��S=-$\frac{3}{2}$t2-$\frac{9}{2}$t+$\frac{9}{2}$+4.5=-$\frac{3}{2}$t2-$\frac{9}{2}$t+9��-3��t��0��
����ͼ3����NI��x���ڵ�I��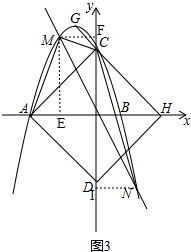 ��
��
���N�������ǣ�t1��p1����
��NI=|t1|��
��S��CMN=S��COM+S��CON=$\frac{3}{2}$��|t|+|t1|����
��t��0��t1��0��
��S��CMN=$\frac{3}{2}$��|t|+|t1|��=$\frac{3}{2}{��t}_{1}-t��$=$\frac{21}{4}$��
${��t}_{1}-t=\frac{7}{2}$��
����$\left\{\begin{array}{l}{y=kx}\\{y={-x}^{2}-2x+3}\end{array}\right.$
�ɵ�x2+��k+2��x-3=0��
��t1��t�Ƿ��̵���������
��$\left\{\begin{array}{l}{{t}_{1}+t=-��k+2��}\\{{t}_{1}t=-3}\end{array}\right.$
��${{��t}_{1}-t��}^{2}$=${{��t}_{1}+t��}^{2}$-4t1t=��k+2��2-4����-3��=${��\frac{7}{2}��}^{2}$=$\frac{49}{4}$��
���${k}_{1}=-\frac{3}{2}$��${k}_{2}=-\frac{5}{2}$��
a��k=-$\frac{3}{2}$ʱ��
��x2+��2-$\frac{3}{2}$��x-3=0��
���x1=-2����${x}_{2}=\frac{3}{2}$����ȥ����
b��k=-$\frac{5}{2}$ʱ��
��x2+��2-$\frac{5}{2}$��x-3=0��
���x3=-$\frac{3}{2}$����x4=2����ȥ����
��t=-2����t=-$\frac{3}{2}$��
t=-2ʱ��
S=-$\frac{3}{2}$t2-$\frac{9}{2}$t+9
=-$\frac{3}{2}$��4-$\frac{9}{2}$����-2��+9
=12
t=-$\frac{3}{2}$ʱ��
S=-$\frac{3}{2}$��$\frac{9}{4}$-$\frac{9}{2}$��$��-\frac{3}{2}��$+9
=$\frac{99}{8}$��
��S��ֵ��12��$\frac{99}{8}$��
���� ��1��������Ҫ�����˶��κ����ۺ��⣬�����˷������������������˷�������˼���Ӧ�ã����������ν�Ϸ�����Ӧ�ã������˴���֪����ͼ���л�ȡ��Ϣ���������û�ȡ����Ϣ�����Ӧ�������������
��2����������˴���ϵ������������ʽ�ķ������Լ����̵ĸ���ϵ���Ĺ�ϵ��Ҫ�������գ�
��3����������������ε���������Լ������ε��ж������ʵ�Ӧ�ã�Ҫ�������գ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
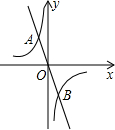 ��ͼ������y1=$\frac{{k}_{1}}{x}$��k1��0����y2=k2x��k2��0����ͼ��Ox����A��B���㣬��A��-1��3������y1��y2����x��ȡֵ��Χ�ǣ�������
��ͼ������y1=$\frac{{k}_{1}}{x}$��k1��0����y2=k2x��k2��0����ͼ��Ox����A��B���㣬��A��-1��3������y1��y2����x��ȡֵ��Χ�ǣ�������| A�� | -1��x��0 | B�� | x��-1��0��x��1 | C�� | -1��x��1 | D�� | -1��x��0��x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
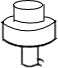 ��ͼ��ʾ��������װ��ˮ������ˮ�ܣ������ڵ�ˮ������������������Һ��ĸ߶�h��ʱ��x�仯�ĺ���ͼ����ӽ�ʵ��������ǣ�������
��ͼ��ʾ��������װ��ˮ������ˮ�ܣ������ڵ�ˮ������������������Һ��ĸ߶�h��ʱ��x�仯�ĺ���ͼ����ӽ�ʵ��������ǣ�������| A�� | 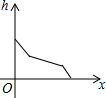 | B�� | 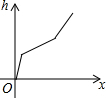 | C�� | 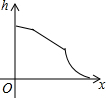 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��������ֽ��ABCD����EF�۵���C��D����ֱ�����C�䡢D���λ�ã��������á�EFB=65�㣬���AED��Ķ����ǣ�������
��ͼ��������ֽ��ABCD����EF�۵���C��D����ֱ�����C�䡢D���λ�ã��������á�EFB=65�㣬���AED��Ķ����ǣ�������| A�� | 65�� | B�� | 55�� | C�� | 50�� | D�� | 25�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com