
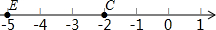 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )| A. | 26 | B. | 27 | C. | 28 | D. | 29 |
分析 根据数轴上点的坐标变化和平移规律(左减右加),分别求出点所对应的数,进而求出点到原点的距离;然后对奇数项、偶数项分别探究,找出其中的规律(相邻两数都相差3),写出表达式;然后根据点到原点的距离不小于41建立不等式,就可解决问题.
解答 解:∵移动1次后该点对应的数为0+1=1,到原点的距离为1;
移动2次后该点对应的数为1-3=-2,到原点的距离为2;
移动3次后该点对应的数为-2+6=4,到原点的距离为4;
移动4次后该点对应的数为4-9=-5,到原点的距离为5;
移动5次后该点对应的数为-5+12=7,到原点的距离为7;
移动6次后该点对应的数为7-15=-8,到原点的距离为8;
…
∴移动(2n-1)次后该点到原点的距离为3n-2;
移动2n次后该点到原点的距离为3n-1.
①当3n-2≥41时,
解得:n≥$\frac{43}{3}$
∵n是正整数,
∴n最小值为15,此时移动了29次.
②当3n-1≥41时,
解得:n≥14.
∵n是正整数,
∴n最小值为14,此时移动了28次.
纵上所述:至少移动28次后该点到原点的距离不小于41,
故选:C.
点评 本题考查了图形的变化及数字的变化规律,考查了数轴上点的坐标变化和平移规律(左减右加),考查了一列数的规律探究.对这列数的奇数项、偶数项分别进行探究是解决这道题的关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2ab)•(-3ab)3=-54a4b3 | B. | (3.5×105)÷(5×106)=7 | ||
| C. | (-0.1b)•(-10b2)3=-b7 | D. | (2×108)($\frac{1}{2}$×1016)=1024 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
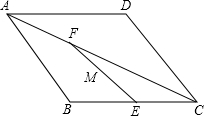 在菱形ABCD中,已知∠ABC=120°,BC=6cm,点E是BC边的中点,F是对角线AC上任意点,现有动点M从点E出发,沿在线段E→F→A移动,在线段EF上的移动速度是1cm/s,在线段FA上的速度是2cm/s,则点M从E到A所需时间的最小值是3$\sqrt{3}$秒.
在菱形ABCD中,已知∠ABC=120°,BC=6cm,点E是BC边的中点,F是对角线AC上任意点,现有动点M从点E出发,沿在线段E→F→A移动,在线段EF上的移动速度是1cm/s,在线段FA上的速度是2cm/s,则点M从E到A所需时间的最小值是3$\sqrt{3}$秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
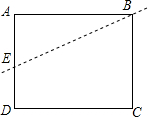 如图,矩形纸片ABCD,AB=10,BC=7,点E在边AD上,沿直线BE折叠纸片,当A对应点A1到边DC的距离为1时,则AE=$\frac{10}{3}$.
如图,矩形纸片ABCD,AB=10,BC=7,点E在边AD上,沿直线BE折叠纸片,当A对应点A1到边DC的距离为1时,则AE=$\frac{10}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com