
已知线段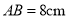 ,在直线
,在直线 上有一点
上有一点 ,且
,且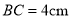 ,点
,点 是线段
是线段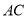 的中点,则线段
的中点,则线段 的长为( ).
的长为( ).
A. 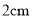 B.
B.  C.
C. 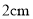 或
或 D.
D.  或
或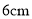
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源:安徽省蚌埠市2017届九年级下学期中考二模数学试卷 题型:单选题
在Rt△ABC中,∠C=90°,AB=10,BC=8,则tanB的值是( )
A.  B.
B. 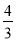 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017-2018学年甘肃省武威市凉州区洪祥镇九年级(上)期末数学试卷 题型:填空题
若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是__.
0或1 【解析】需要分类讨论:①若m=0,则函数为一次函数;②若m≠0,则函数为二次函数,由抛物线与x轴只有一个交点,得到根的判别式的值等于0,且m不为0,即可求出m的值. 【解析】 ①若m=0,则函数y=2x+1,是一次函数,与x轴只有一个交点; ②若m≠0,则函数y=mx2+2x+1,是二次函数. 根据题意得:△=4﹣4m=0, 解得:m=1. 所以当m的...查看答案和解析>>
科目:初中数学 来源:浙江杭州建德2016-2017学年七年级上学期期末数学试卷 题型:解答题
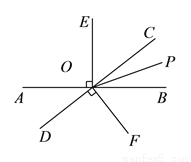
如图,直线 与
与 相交于点
相交于点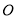 ,
, 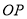 是
是 的平分线,
的平分线, 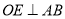 ,
,  .
.
(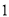 )图中除直角外,还有相等的角吗?请写出三对.
)图中除直角外,还有相等的角吗?请写出三对.
( )如果
)如果 ,求
,求 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源:浙江杭州建德2016-2017学年七年级上学期期末数学试卷 题型:填空题
杭黄高铁全长 公里,预计在
公里,预计在 年建成,到时建德人去杭州从建德东上车经过桐庐站、富阳站、萧山站,最后到达杭州东站,那么铁路总局在这些站应该印制_________种车票.
年建成,到时建德人去杭州从建德东上车经过桐庐站、富阳站、萧山站,最后到达杭州东站,那么铁路总局在这些站应该印制_________种车票.
查看答案和解析>>
科目:初中数学 来源:浙江杭州建德2016-2017学年七年级上学期期末数学试卷 题型:单选题
如果 ,下列成立的是( ).
,下列成立的是( ).
A.  B.
B.  C.
C.  D.
D. 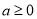
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册 期中测试卷 题型:解答题
如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
(1)如果 ,DE=6,求边BC的长;
,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.

查看答案和解析>>
科目:初中数学 来源:人教版九年级下册 期中测试卷 题型:单选题
如图,双曲线 (k≠0)上有一点A,过点A作AB⊥x轴于点B,△AOB的面积为2,则该双曲线的表达式为( )
(k≠0)上有一点A,过点A作AB⊥x轴于点B,△AOB的面积为2,则该双曲线的表达式为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:单选题
如图,长度为18cm的线段AB的中点为M,点C是线段MB的一个三等分点,则线段AC的长为( )

A. 3cm B. 6cm C. 9cm D. 12cm
D 【解析】∵M是线段AB的中点, ∴BM=AB. 又∵AB=18cm, ∴BM=9cm, ∵C是线段BM的三等分点, ∴BC=BM=6cm, ∴AC=AB-BC=12cm. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com