
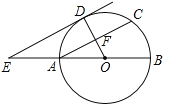
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交![]() 于点D,过点D作⊙O的切线,交BA的延长线于点E.
于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=a,写出求四边形ACDE面积的思路.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)欲证明AC∥DE,只要证明AC⊥OD,ED⊥OD即可.
(2)作DM⊥OA于M,连接CD,CO,AD,首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AEDM,只要求出DM即可.
试题解析:(1)∵ED与⊙O相切于D,∴OD⊥DE,∵F为弦AC中点,∴OD⊥AC,∴AC∥DE.
(2)作DM⊥OA于M,连接CD,CO,AD.
首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AEDM,只要求出DM即可.
∵AC∥DE,AE=AO,∴OF=DF,∵AF⊥DO,∴AD=AO,∴AD=AO=OD,∴△ADO是等边三角形,同理△CDO也是等边三角形,∴∠CDO=∠DOA=60°,AE=CD=AD=AO=DD=a,∴AO∥CD,又AE=CD,∴四边形ACDE是平行四边形,易知DM=![]() ,∴平行四边形ACDE面积=
,∴平行四边形ACDE面积=![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】东营市出租车的收费标准是:起步价8元(即行驶距离不超过3 km都需付8元车费),超过3 km以后,每增加1 km,加收1.5元(不足1 km按1 km计).某人从甲地到乙地经过的路程是x km,出租车费用为15.5元,那么x的最大值是( )
A.11
B.8
C.7
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 绝对值等于本身的数是正数 B. 0除以任何一个数,其商为0
C. 倒数等于本身的数是1 D. 0乘以任何一个数,其积为0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com