
 定义:在平面直角坐标系xOy中,给定两点M(xM,yM),N(xN,yN),对于给定的实数a,b,作a|xM-xN|+b|yM-yN|为M,N的权重为a,b的直角距离,记为dxy(M,N),例如:d2,3((1,0),(4,7))=2|1-4|+3|0-7|=27.
定义:在平面直角坐标系xOy中,给定两点M(xM,yM),N(xN,yN),对于给定的实数a,b,作a|xM-xN|+b|yM-yN|为M,N的权重为a,b的直角距离,记为dxy(M,N),例如:d2,3((1,0),(4,7))=2|1-4|+3|0-7|=27.分析 (1)根据给定的实数a,b,作a|xM-xN|+b|yM-yN|为M,N的权重为a,b的直角距离,记为dxy(M,N),可得答案;
(2)由于P在直线y=2x+4上,所以可以先设P(x,2x+4),用x表示出OP的等权重距离,由于结果带绝对值,所以需分类讨论,从而得出最小值,最后求P的坐标;
(3)根据解方程组,可得OP与等圆的交点Q,根据权重为1、1的直角距离,又称为等权重距离,则记为d(M,N),可得答案,根据a|xM-xN|+b|yM-yN|为M,N的权重为a,b的直角距离,记为dxy(M,N),可得答案.
解答 解:(1)d((0,0),(-3,-2))=|0+3|+|0+2|=5,
d3,2((0,0),(-1,2))=3|0-(-1)|+2|0-2|=7,
故答案为:5,7;
(2)设P坐标为(x,2x+4),则:
d((0,0),(x,2x+4))=|x|+|2x+4|.
直线y=2x+4与x轴的交点为(-2,0)
①当x≥0时,d((0,0),(x,2x+4))=|x|+|2x+4|=x+2x+4=3x+4≥4;
②当-2≤x<0时,d((0,0),(x,2x+4))=|x|+|2x+4|=-x+2x+4=x+4,此时2≤d((0,0),(x,2x+4))<4;
③当x<-2时,d((0,0),(x,2x+4))=|x|+|2x+4|=-x-2x-4=-3x-4>2.
即当x=-2时,OP的等权重距离的最小值,此时P(-2,0)
(3)如图2: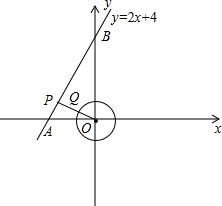 ,
,
由(2)知P(-$\frac{8}{5}$,$\frac{4}{5}$),
联立OP、单位圆,得
$\left\{\begin{array}{l}{y=-\frac{1}{2}x}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-\frac{2\sqrt{5}}{5}}\\{y=\frac{\sqrt{5}}{5}}\end{array}\right.$,
即Q(-$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$),
d(P,Q)的最小值是=|-$\frac{8}{5}$-(-$\frac{2\sqrt{5}}{5}$)|+|$\frac{4}{5}$-$\frac{\sqrt{5}}{5}$|=$\frac{8}{5}$-$\frac{2\sqrt{5}}{5}$+$\frac{4}{5}$-$\frac{\sqrt{5}}{5}$=$\frac{12}{5}$-$\frac{3\sqrt{5}}{5}$,
d3,2(P,Q)的最小值是=3|-$\frac{8}{5}$-(-$\frac{2\sqrt{5}}{5}$)|+2|$\frac{4}{5}$-$\frac{\sqrt{5}}{5}$|=$\frac{24}{5}$-$\frac{6\sqrt{5}}{5}$+$\frac{8}{5}$-$\frac{2\sqrt{5}}{5}$=$\frac{32}{5}$-$\frac{8\sqrt{5}}{5}$,
故答案为:$\frac{12}{5}$-$\frac{3\sqrt{5}}{5}$,$\frac{32}{5}$-$\frac{8\sqrt{5}}{5}$.
点评 本题考查了一次函数综合题,利用了a|xM-xN|+b|yM-yN|为M,N的权重为a,b的直角距离,记为dxy(M,N),垂线段的性质,解方程组,确定Q、P点坐标是解题关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源:2016-2017学年江苏省八年级下学期第一次月考数学试卷(解析版) 题型:填空题
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′= .

查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中复习检测数学试卷(一)(解析版) 题型:解答题
太仓港区道路绿化工程工地有大量货物需要运输,某车队有载重量为8吨和10吨的卡车共15辆,所有车辆运输一次能运输128吨货物.
(1)求该车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的扩大,车队需要一次运输货物170吨以上,为了完成任务,车队准备增购这两种卡车共5辆(两种车都购买),请写出所有可能的购车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
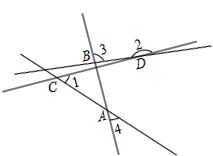 已知平面直角坐标系内点A(m,n),将点A向上平移4个单位,向左平移1个单位得到点B,再向下平移2个单位,向左平移3个单位得到点C,再将C向上平移3个单位,向右平移7个单位得到点D,且D(2n,2-4m),连接直线AC,DC,AB,BD,得到如图所示.
已知平面直角坐标系内点A(m,n),将点A向上平移4个单位,向左平移1个单位得到点B,再向下平移2个单位,向左平移3个单位得到点C,再将C向上平移3个单位,向右平移7个单位得到点D,且D(2n,2-4m),连接直线AC,DC,AB,BD,得到如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小华在罚球线上连续投篮5次,一定能投中3次 | |
| B. | 小华在罚球线上连续投篮5次,有投中3次的可能性 | |
| C. | 小华在罚球线上投篮1次,投中的可能性较大 | |
| D. | 小华在罚球线上投篮1次,投不中的可能性较小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com