
【题目】图a是一个长为2m、宽为2n的长方形,沿图中实现用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.

(1)图b中,大正方形的边长是 .阴影部分小正方形的边长是 ;
(2)观察图b,写出(m+n)2,(m﹣n)2,mn之间的一个等量关系,并说明理由.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,∠BAC和∠DAE都是70°30′的角.
(1)如果∠DAC=27°30′,那么∠BAE等于多少度?(写出过程)
(2)请写出图中相等的角;
(3)若∠DAC变大,则∠BAD如何变化?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B(1,3),C(1,0),直线y=x+k经过点B,且与x轴交于点A,将△ABC沿直线AB折叠得到△ABD.
(1)填空:A点坐标为( , ),D点坐标为( , );
(2)若抛物线y= ![]() x2+bx+c经过C,D两点,求抛物线的解析式;
x2+bx+c经过C,D两点,求抛物线的解析式;
(3)将(2)中的抛物线沿y轴向上平移,设平移后所得抛物线与y轴交点为E,点M是平移后的抛物线与直线AB的公共点,在抛物线平移过程中是否存在某一位置使得直线EM∥x轴.若存在,此时抛物线向上平移了几个单位?若不存在,请说明理由.
(提示:抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣ ![]() ,顶点坐标是(﹣
,顶点坐标是(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
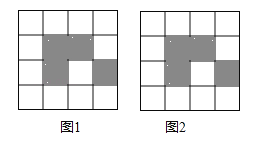
【题目】如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=![]() ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点的初始位置位于数轴上表示1的点,现对A点做如下移动:第1次向左移动3个单位长度至B点,第2次从B点向右移动6个单位长度至C点,第3次从C点向左移动9个单位长度至D点,第4次从D点向右移动12个单位长度至E点,…,依此类推.这样第_____次移动到的点到原点的距离为2018.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.8的立方根是±2
B.![]() 是一个最简二次根式
是一个最简二次根式
C.函数y= ![]() 的自变量x的取值范围是x>1
的自变量x的取值范围是x>1
D.在平面直角坐标系中,点P(2,3)与点Q(﹣2,3)关于y轴对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com