
【题目】如图,已知△ABC中,AB=AC,BE平分∠ABC交AC于E,若∠A=90°,那么BC、BA、AE三者之间有何关系?并加以证明.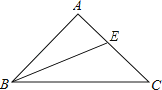
【答案】解:BC、BA、AE三者之间的关系:BC=BA+AE,理由如下:
过E作ED⊥BC交BC于点D,∵BE平分∠ABC,BA⊥CA,∴AE=DE,∠EDC=∠A=∠BDE=90°,∵在Rt△BAE和Rt△BDE中,BE=BE,AE=DE,∴Rt△BAE≌Rt△BDE(HL),
∴BA=BD,∵AB=AC,∠A=90°∴∠C=45°,∴∠CED=45°=∠C,∴DE=CD,∵AE=DE,
∴AE=CD=DE,∴BC=BD+DC=BA+AE.
【解析】先根据直角三角形的判定Rt△BAE≌Rt△BDE,再根据角平分线的性质进行等量代换.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6㎝, △DEB的周长为( )21co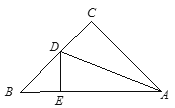
A.4cm
B.6cm
C.10cm
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于按固定顺序的![]() 个数:
个数: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,称为数列
,称为数列![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 为整数且
为整数且![]() .
.
定义![]() .
.
例如,若数列![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,则
,则![]() .
.
根据以上材料,回答下列问题:
(![]() )已知数列
)已知数列![]() ,
, ![]() ,
, ![]() ,求
,求![]() .
.
(![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 中
中![]() 个数均为非负数,且
个数均为非负数,且![]() ,直接写出
,直接写出![]() 的最大值和最小值.
的最大值和最小值.
(![]() )已知数列
)已知数列![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() ,
, ![]() ,为
,为![]() 个整数,且
个整数,且![]() ,
, ![]() ,
, ![]() ,直接写出所有可能的数列
,直接写出所有可能的数列![]() 中至少两种.
中至少两种.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC底边BC的长为4cm,面积是12cm2 , 腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最小值为cm. 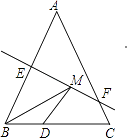
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com