
【题目】如图,![]() 、
、![]() 、
、![]() 三点在同一条直线上,
三点在同一条直线上,![]() 和
和![]() 是等边三角形,
是等边三角形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
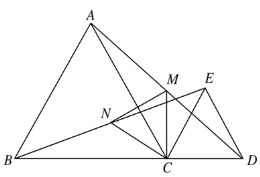
求证:(1)![]() ;
;
(2)![]() 是等边三角形.
是等边三角形.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)由两三角形为等边三角形,得到两对边相等,一对角为60度,利用等式的性质得到夹角相等,利用SAS得到三角形ACD与三角形BCE全等;
(2)利用全等三角形的对应角相等得到一对角相等,再由两个角为60度,且夹边AC=BC,利用SAS得到三角形ACM与三角形BCN全等,利用全等三角形对应边相等即可得证.
证明:
(1)∵△ABC与△ECD均为等边三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE,
在△ACD和△BCE中,
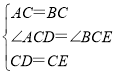 ,
,
∴△ACD≌△BCE(SAS),
∴![]()
(2)由(1)可得![]() ,∠DAC=∠EBC
,∠DAC=∠EBC
∵M、N分别为AD、BE的中点
∴AM=BN
又AC=BC
∴△ACM≌△BCN(SAS)
∴MC=NC,∠ACM=∠BCN
∴∠MCN=∠ACM+∠ACN=∠BCN+∠ACN=∠ACB=60°
∴![]() 是等边三角形
是等边三角形


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,直线l1:y=kx+4与y轴交于点A,与x轴交于点B.
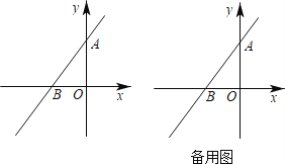
(1)请直接写出点A的坐标:______;
(2)点P为线段AB上一点,且点P的横坐标为m,现将点P向左平移3个单位,再向下平移4个单位,得点P′在射线AB上.
①求k的值;
②若点M在y轴上,平面内有一点N,使四边形AMBN是菱形,请求出点N的坐标;
③将直线l1绕着点A顺时针旋转45°至直线l2,求直线l2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若k=3,a=﹣![]() ,则喷出的抛物线水线能否达到岸边?
,则喷出的抛物线水线能否达到岸边?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)
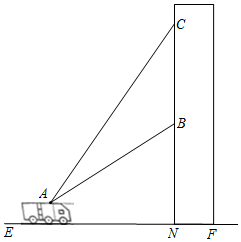
查看答案和解析>>
科目:初中数学 来源: 题型:
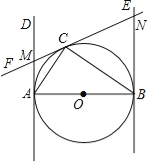
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.
(1)求证:PA平分∠BAC的外角∠CAM;
(2)过点C作CE⊥AP,E是垂足,并延长CE交BM于点D.求证:CE=ED.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字2,1,﹣3,﹣4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为m,再随机地摸取一张,将卡片上的数字记为n.
(1)请画出树状图并写出(m,n)所有可能的结果;
(2)求所选出的m,n能使一次函数y=mx+n的图象经过第二、三、四象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com