
分析 (1)先估算出$\sqrt{5}$的范围,即可得出答案;
(2)先估算出$\sqrt{2}$的范围,即可得出答案;
(3)先求出1+$\sqrt{2}$+$\sqrt{3}$的范围,即可得出答案;
(4)先求出2+$\sqrt{3}$的范围,求出x、y,即可得出答案.
解答 解:(1)∵2<$\sqrt{5}$<3,
∴$\sqrt{5}$的整数部分是2,小数部分为$\sqrt{5}$-2,
故答案为:2,$\sqrt{5}$-2;
(2)∵1<$\sqrt{2}$<2,
∴2<1+$\sqrt{2}$<3,
∴1+$\sqrt{2}$的整数部分是2,小数部分是1+$\sqrt{2}$-2=$\sqrt{2}$-1,
故答案为:2,$\sqrt{2}$-1;
(3)∵2.4<1+$\sqrt{2}$<3,1.7$<\sqrt{3}<2$,
∴4.1<1+$\sqrt{2}$+$\sqrt{3}$<5,
∴1+$\sqrt{2}$+$\sqrt{3}$,的整数部分是4,小数部分是$\sqrt{2}$+$\sqrt{3}$-3,
故答案为:4,$\sqrt{2}$+$\sqrt{3}$-3;
(4)∵1<$\sqrt{3}$<2,
∴3<2+$\sqrt{3}$<4,
∴x=3,y=$\sqrt{3}$-1,
∴x-$\sqrt{3}$y=3-$\sqrt{3}$($\sqrt{3}$-1)=$\sqrt{3}$.
点评 本题考查了估算无理数的大小,能正确估算出每个无理数的大小是解此题的关键.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≥-$\frac{2}{3}$ | B. | a≥2 | C. | a<-$\frac{2}{3}$ | D. | a≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
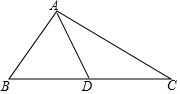 如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=$\frac{11}{10}$,则tan∠BAD=$\frac{33}{10}$.
如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=$\frac{11}{10}$,则tan∠BAD=$\frac{33}{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
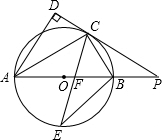 如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率 $\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
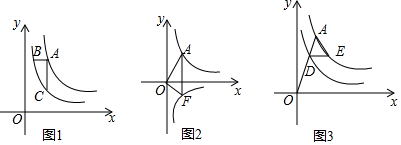
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com