
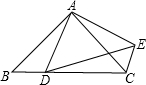
 如图,D为等腰直角三角形斜边BC上的一点,△ABD绕点A旋转后与△ACE重合,如果AD=1,那么DE=
如图,D为等腰直角三角形斜边BC上的一点,△ABD绕点A旋转后与△ACE重合,如果AD=1,那么DE= 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 抛物线的对称轴为直线x=m.求当k为何值时,|m|=
抛物线的对称轴为直线x=m.求当k为何值时,|m|=| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 所示的等腰直角三角形BCD,点E在过A、C、D三点的圆上,且DE⊥BD,连结CE、AD.
所示的等腰直角三角形BCD,点E在过A、C、D三点的圆上,且DE⊥BD,连结CE、AD.查看答案和解析>>
科目:初中数学 来源: 题型:
 为等腰直角三角形
为等腰直角三角形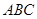 的重心,
的重心, ,直线
,直线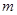 过点
过点 ,过
,过 三点分别作直线
三点分别作直线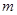 的垂线,垂足分别为点
的垂线,垂足分别为点 .
. 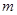 与
与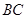 平行时(图1),请你猜想线段
平行时(图1),请你猜想线段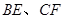 和
和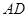 三者之间的数量关系并证明;
三者之间的数量关系并证明;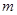 绕点
绕点 旋转到与
旋转到与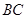 不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段
不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段 三者之间又有怎样的数量关系?请写出你的结论,不需证明.
三者之间又有怎样的数量关系?请写出你的结论,不需证明.
查看答案和解析>>
科目:初中数学 来源:2011-2012年北京二龙路中学九年级第一学期期中测试数学卷 题型:解答题
我们知道三角形三条中线的交点叫做三角形的重心.经过证明我们可得三角形重心具备下面的性质: 重心到顶点的距离与重心到该顶点对边中点的距离之比为2﹕1.请你用此性质解决下面的问题.
已知:如图,点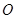 为等腰直角三角形
为等腰直角三角形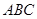 的重心,
的重心,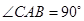 ,直线
,直线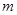 过点
过点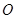 ,过
,过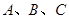 三点分别作直线
三点分别作直线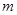 的垂线,垂足分别为点
的垂线,垂足分别为点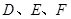 .
.
<1>当直线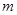 与
与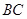 平行时(图1),请你猜想线段
平行时(图1),请你猜想线段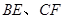 和
和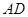 三者之间的数量关系并证明;
三者之间的数量关系并证明;
<2>当直线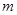 绕点
绕点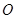 旋转到与
旋转到与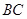 不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段
不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段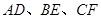 三者之间又有怎样的数量关系?请写出你的结论,不需证明.
三者之间又有怎样的数量关系?请写出你的结论,不需证明.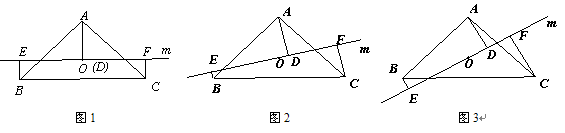
查看答案和解析>>
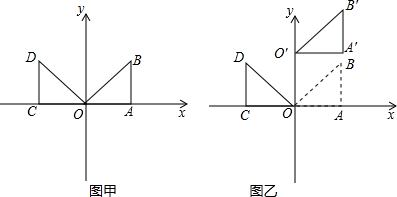
科目:初中数学 来源:2012年苏教版初中数学八年级上5.1函数练习卷(解析版) 题型:选择题
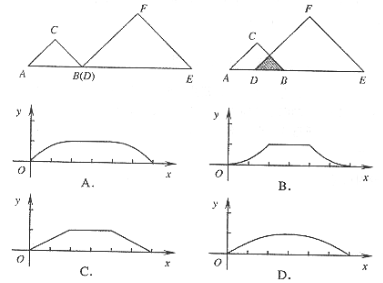
如图,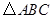 和的
和的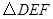 是等腰直角三形,
是等腰直角三形,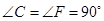 ,
,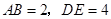 .点B与点D重合,点
.点B与点D重合,点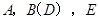 在同一条直线上,将
在同一条直线上,将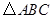 沿
沿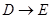 方向平移,至点
方向平移,至点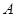 与点
与点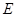 重合时停止.设点
重合时停止.设点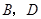 之间的距离为x,
之间的距离为x,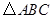 与
与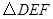 重叠部分的面积为
重叠部分的面积为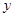 ,则准确反映
,则准确反映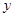 与
与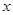 之间对应关系的图象是( )
之间对应关系的图象是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com