
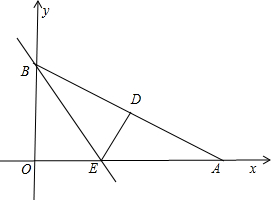
 重合,点A在x轴上,点B在y轴上
重合,点A在x轴上,点B在y轴上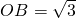 ,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.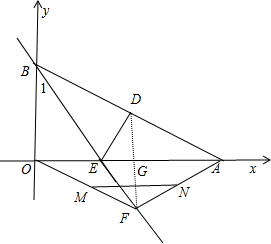 解:(1)据题意可得∠1=
解:(1)据题意可得∠1=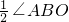 ,OB=BD=
,OB=BD= ,DE=OE,
,DE=OE, ,
, ).
).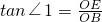
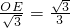
 ),
), OA=1.5,DG=
OA=1.5,DG= OB=
OB= ;
; ).
). )代入y=a(x-0)(x-3)
)代入y=a(x-0)(x-3)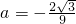 ,
,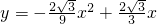 .
. )和(1,0)分别代入y=k1x+b1
)和(1,0)分别代入y=k1x+b1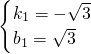 ,
,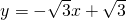 ,
,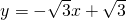 得:
得: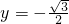 ,
, ),M点坐标为(
),M点坐标为( ,-
,- ),N点坐标为(
),N点坐标为( ,-
,- ),
), ,
, ),
), ,
, )和(
)和( ,-
,- )分别代入y=k2x+b2
)分别代入y=k2x+b2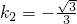 ,
,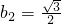 ,
,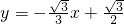 ,
,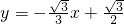
 ,
, ,0),
,0),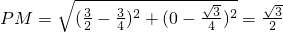 ,
,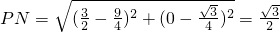 ,
,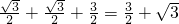 .
.

科目:初中数学 来源: 题型:
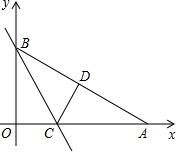 如图,Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上,OB=
如图,Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上,OB=| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
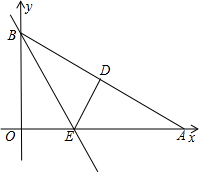 痕为BE.
痕为BE.查看答案和解析>>
科目:初中数学 来源: 题型:
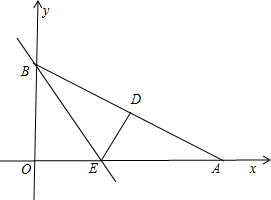 重合,点A在x轴上,点B在y轴上OB=
重合,点A在x轴上,点B在y轴上OB=| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
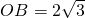 ,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折
,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折 痕为BE.
痕为BE.查看答案和解析>>
科目:初中数学 来源:山东省中考真题 题型:解答题
 ,∠BAO=30度,将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC。
,∠BAO=30度,将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com