
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)= ![]() .例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)=
.例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)= ![]() .
.
(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数.则对任意一个完全平方数m,F(m)=;
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的值.
【答案】
(1)1
(2)
解:设交换t的个位上的数与十位上的数得到的新数为t′,则t′=10y+x,
∵t为“吉祥数”,
∴t′﹣t=(10y+x)﹣(10x+y)=9(y﹣x)=18,
∴y=x+2,
∵1≤x≤y≤9,x,y为自然数,
∴“吉祥数”有:13,24,35,46,57,68,79,
∴所有“吉祥数”中F(t)的值为:F(13)= ![]() ,F(24)=
,F(24)= ![]() =
= ![]() ,F(35)=
,F(35)= ![]() ,F(46)=
,F(46)= ![]() ,F(57)=
,F(57)= ![]() ,F(68)=
,F(68)= ![]() ,F(79)=
,F(79)= ![]()
【解析】解:(1)对任意一个完全平方数m,设m=n2(n为正整数),
∵|n﹣n|=0,
∴n×n是m的最佳分解,
∴对任意一个完全平方数m,F(m)= ![]() =1;
=1;
所以答案是:1;
【考点精析】解答此题的关键在于理解数与式的规律的相关知识,掌握先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】要调查下列问题,你认为哪些适合抽样调查:①了解全国手机用户对废手机的处理情况;②检测某地区空气的质量;③调查全市中学生一天的学习时间( )
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】马师傅计划用10天时间完成加工320个零件,前二天每天加工20个零件,后改进了工作方式,结果提前一天并超额完成了加工任务,若设马师傅在二天后每天至少加工x个零件,请你列出x所满足的不等式并求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2πr)
(1)把圆片沿数轴向左滚动1周,点Q到达数轴上点A的位置,点A表示的数是;
(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:
+2,﹣1,﹣5,+4,+3,﹣2
①第几次滚动后,Q点距离原点最近?第几次滚动后,Q点距离原点最远?
②当圆片结束运动时,Q点运动的路程共有多少?此时点Q所表示的数是多少?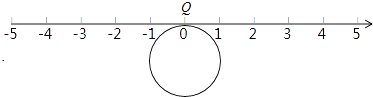
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A(3,y1),B(5,y2),C(﹣2,y3)是抛物线y=﹣x2+4x+k上的三点,则y1、y2、y3的大小关系为( )
A.y2>y1>y3
B.y3>y2>y1
C.y1>y2>y3
D.y3>y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
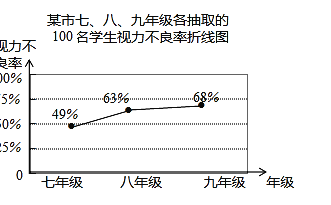
【题目】为了解某市12000名初中学生的视力情况,该校数学兴趣小组从该市七、八、九年级各随机抽取了100名学生进行调查,整理他们的视力情况数据,得到如下的折线统计图.
(1)由统计图可以看出年级越高视力不良率越 (填“高”或“低”);
(2)抽取的八年级学生中,视力不良的学生有 名;
(3)请你根据抽样调查的结果,估计该市12000名初中学生中视力不良的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
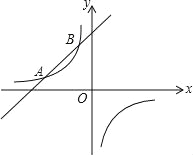
【题目】如图,已知反比例函数y1=![]() (k≠0)的图象经过点(8,-
(k≠0)的图象经过点(8,-![]() ),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).
),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).
(1)求上述反比例函数和直线的解析式;
(2)当y1<y2时,请直接写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com