
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:解答题
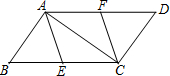 如图,已知点E、点F分别是平行四边形ABCD的边BC、AD上的中点,AC是
如图,已知点E、点F分别是平行四边形ABCD的边BC、AD上的中点,AC是查看答案和解析>>
科目:初中数学 来源: 题型:解答题
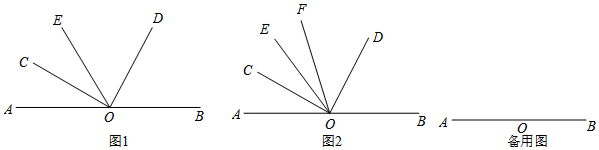
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
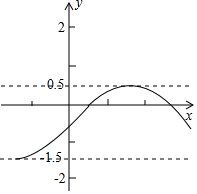 对于某一函数,给出如下定义:若存在实数M>0,对于一函数任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的确界值.例如如图所示的函数是有界函数,其确界值是1.5.问:将函数y=-x2(-m≤x≤1,m≥o)的图象向上平移m个单位,得到的函数的确界值是t,当m在什么范围时,满足$\frac{3}{4}≤t≤1$.
对于某一函数,给出如下定义:若存在实数M>0,对于一函数任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的确界值.例如如图所示的函数是有界函数,其确界值是1.5.问:将函数y=-x2(-m≤x≤1,m≥o)的图象向上平移m个单位,得到的函数的确界值是t,当m在什么范围时,满足$\frac{3}{4}≤t≤1$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com