
 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
 降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价-进货价)
降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价-进货价)查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分10分)南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价![]() 万元,每辆汽车的销售利润为
万元,每辆汽车的销售利润为![]() 万元.(销售利润
万元.(销售利润![]() 销售价
销售价![]() 进货价)
进货价)
(1)求![]() 与
与![]() 的函数关系式;在保证商家不亏本的前提下,写出
的函数关系式;在保证商家不亏本的前提下,写出![]() 的取值范围;
的取值范围;
(2)假设这种汽车平均每周的销售利润为![]() 万元,试写出
万元,试写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源:2012届江苏省泰州市苏陈中学九年级下学期质量检测数学卷 题型:解答题
(本题满分10分)南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价 万元,每辆汽车的销售利润为
万元,每辆汽车的销售利润为 万元.(销售利润
万元.(销售利润 销售价
销售价 进货价)
进货价)
(1)求 与
与 的函数关系式;在保证商家不亏本的前提下,写出
的函数关系式;在保证商家不亏本的前提下,写出 的取值范围;
的取值范围;
(2)假设这种汽车平均每周的销售利润为 万元,试写出
万元,试写出 与
与 之间的函数关系式;
之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省泰州市九年级下学期质量检测数学卷 题型:解答题
(本题满分10分)南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价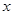 万元,每辆汽车的销售利润为
万元,每辆汽车的销售利润为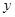 万元.(销售利润
万元.(销售利润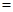 销售价
销售价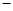 进货价)
进货价)
(1)求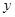 与
与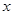 的函数关系式;在保证商家不亏本的前提下,写出
的函数关系式;在保证商家不亏本的前提下,写出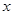 的取值范围;
的取值范围;
(2)假设这种汽车平均每周的销售利润为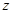 万元,试写出
万元,试写出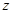 与
与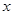 之间的函数关系式;
之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》中考题集(23):20.5 二次函数的一些应用(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com