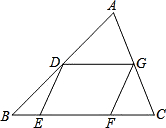
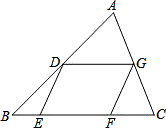
(1)解:∵D、G分别是AB、AC的中点,
∴DG∥BC,且DG=

BC.
分别过点A、D作AM⊥BC,DN⊥BC,如图,
则∠DNB=∠AMB.
∴△DNB∽△AMB.
又∵DB=

AB,
∴DN=

AM.
∴T=

S.
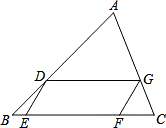
(2)证明:过点G作GH∥AB,交BC于点H,如图,
则∠B=∠GHF.
∵DE=GF,DE∥GF,所以∠DEB=∠GFH.
∴△DBE≌△GHF.
∵DG∥BC,

∴△ADG∽△ABC.
同理,△GHC∽△ABC.
设AD=k•AB(0<k<1),则S
△ADG=k
2S.
同理,S
△GHC=(1-k)
2S.
T=S-S
△ADG-S
△GHC=[1-k
2-(1-k)
2]S
=(-2k
2+2k)S=-2[(k-

)
2-

]S
=-2(k-

)
2S+

S≤

S.
(3)证明:分以下四种情形讨论:
第一种情形:如果剪得的平行四边形有三个顶点在三角形的边上,第四个顶点不在三角形的边上.
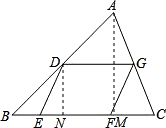
①当其中有两个顶点在同一边时,如图所示,延长DG交AC于点G′,过点G′作G′F′∥GF,交BC于点F′,易知四边形DEF′G′是平行四边形,则T≤S
□DEF′G′.

由(2)知,S
□DEF′G′≤

S.
所以T≤

S.
②当三点分别在三角形的三边时,如图过A点作AH∥DE交EF、DG于F′、G′,问题转化为(2)和图3-1两
种情形,则
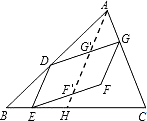
T=S
□DEF′G’’+S
□F′G′GF≤

S
△ABH+

S
△AHC=

S.
第二种情形:如果剪得的平行四边形有两个顶点在三角形的边上,另两个顶点不在三角形的边上.
①当这两个顶点在同一边上时,如图,延长DG与三角形的两边AB、AC分别交于点L、K,作平行四边形MNKL.
问题转化为(2).则
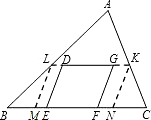
T=S
□DEFG≤S
□MNKL≤

S.
②当这两个顶点分别在三角形的两边上时,如图.延长DE、GF交BC于点K、M,过点K作KN∥DG,交GM于点N.易
得四边形DKNG是平行四边形,从而问题转化为图3-2的情形,则
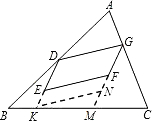
T=S
□DEFG≤S
□DKN′G≤

S.
第三种情形:如果剪得的平行四边形只有一个顶点在三角形的边上,另三个顶点不在三角形的边上.如图,延长ED、
FG分别交AB、AC于点K、M,过点K作KN∥DG,交FM于点N.易得四边形EFNK是平行四边形,从而问题转化为图3-4
的情形,则
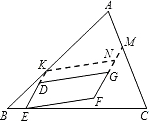
T=S
□DEFG≤S
□EFNK≤

S
第四种情形:如果剪得的平行四边形没有顶点在三角形的边上时,如图,延长ED、FG分别交AB、AC于点K、
M,过点K作KN∥DG,交FM于点N.易得四边形EFNK是平行四边形,从而问题转化为下图的情形,则
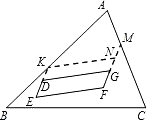
T=S
□DEFG≤S
□EFNK≤

S.
综上,对任意剪得的□DEFG,T≤

S成立.
分析:(1)由D、G分别是AB、AC的中点,得DG∥BC,且DG=

BC.分别过点A、D作AM⊥BC,DN⊥BC,得△DNB∽△AMB,则DB=

AB,DN=

AM.即可得到T=

S.
(2)过点G作GH∥AB,交BC于点H,易得△DBE≌△GHF.△ADG∽△ABC,△GHC∽△ABC,设AD=k•AB(0<k<1),则S
△ADG=k
2S.同理,S
△GHC=(1-k)
2S.则T=S-S
△ADG-S
△GHC=[1-k
2-(1-k)
2]S,利用配方即可得到T≤

S;
(3)分以下四种情形讨论:
第一种情形:如果剪得的平行四边形有三个顶点在三角形的边上,第四个顶点不在三角形的边上.
①当其中有两个顶点在同一边时,如图所示,延长DG交AC于点G′,过点G′作G′F′∥GF,交BC于点F′,易知四边形DEF′G′是平行四边形,则T≤S
□DEF′G′.
②当三点分别在三角形的三边时,如图过A点作AH∥DE交EF、DG于F′、G′,问题转化为(2)和图3-1两
种情形,则T=S
□DEF′G’’+S
□F′G′GF≤

S
△ABH+

S
△AHC=

S.
第二种情形:如果剪得的平行四边形有两个顶点在三角形的边上,另两个顶点不在三角形的边上.
转化为第一种情形证明.
点评:本题考查了三角形相似的判定与性质:平行于三角形一边的直线与其它两边相交所截得的三角形与原三角形相似;也考查了三角形中位线性质以及三角形的面积公式.

 S;
S;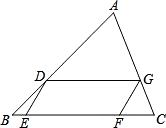
 S还成立吗?请说明理由.
S还成立吗?请说明理由. (1)解:∵D、G分别是AB、AC的中点,
(1)解:∵D、G分别是AB、AC的中点, BC.
BC. AB,
AB, AM.
AM. S.
S.
 )2-
)2- ]S
]S )2S+
)2S+ S≤
S≤ S.
S.
 S.
S. S.
S.
 S△ABH+
S△ABH+ S△AHC=
S△AHC= S.
S.
 S.
S.
 S.
S.
 S
S
 S.
S. S成立.
S成立. BC.分别过点A、D作AM⊥BC,DN⊥BC,得△DNB∽△AMB,则DB=
BC.分别过点A、D作AM⊥BC,DN⊥BC,得△DNB∽△AMB,则DB= AB,DN=
AB,DN= AM.即可得到T=
AM.即可得到T= S.
S. S;
S; S△ABH+
S△ABH+ S△AHC=
S△AHC= S.
S.