
【题目】如图,将![]() 沿过点
沿过点![]() 的直线
的直线![]() 折叠,使点
折叠,使点![]() 落到
落到![]() 边上的
边上的![]() 处,折痕交
处,折痕交![]() 边于点
边于点![]() ,连接
,连接![]() .
.
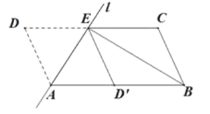
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() 平分
平分![]() ,求证:
,求证:![]() .
.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形;
(2)利用平行线的性质结合勾股定理得出答案.
(1)∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴CE ∥D′B,
∴四边形BCED′是平行四边形;
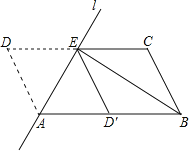
(2)∵BE平分∠ABC,
∴∠CBE=∠EBA,
∵AD∥BC,
∴∠DAB+∠CBA=180°,
∵∠DAE=∠BAE,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°,
∴AB2=AE2+BE2.


科目:初中数学 来源: 题型:
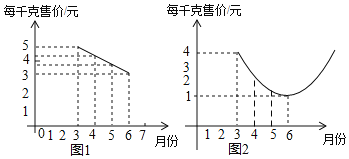
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3 月初某商品价格上涨,每件价格上涨 20%.用 3000 元买到的该商品 件数比涨价前少 20 件.3 月下旬该商品开始降价,经过两次降价后,该商品价格为每 件 19.2 元.
(1)求 3 月初该商品上涨后的价格;
(2)若该商品两次降价率相同,求该商品价格的平均降价率.
查看答案和解析>>
科目:初中数学 来源: 题型:
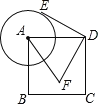
【题目】如图,已知正方形 ABCD 的边长为 2,以点 A 为圆心,1 为半径作圆,点 E 是⊙A 上的任意 一点,点 E 绕点 D 按逆时针方向转转 90°,得到点 F,接 AF,则 AF 的最大值是______________
查看答案和解析>>
科目:初中数学 来源: 题型:
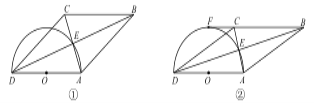
【题目】四边形 ABCD 的对角线交于点 E,且 AE=EC,BE=ED,以 AD 为直径的半圆过点 E,圆心 为 O.
(1)如图①,求证:四边形 ABCD 为菱形;
(2)如图②,若 BC 的延长线与半圆相切于点 F,且直径 AD=6,求弧AE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC底边BC上的高为16 cm,当BC的长x(cm)从小到大变化时,△ABC的面积y(cm2)也随之发生变化.
(1)在这个变化过程中,常量是________,自变量是________,因变量是_________;
(2)写出y与x之间的关系式为_______________;
(3)当x=5 cm时,y=________cm2;当x=15 cm时,y=________cm2;y随x的增大而__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
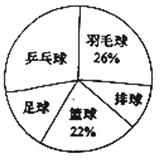
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com