
ЁОЬтФПЁПЬНОПгыЗЂЯжЃКШчЭМЃЈ1ЃЉЫљЪОЕФЭМаЮЃЌЯёЮвУЧГЃМћЕФбЇЯАгУЦЗвЛдВЙцЃЌЮвУЧЃЌВЛЗСАбетбљЭМаЮНазіЁАЙцаЮЭМ
ЃЈ1ЃЉЙлВьЁАЙцаЮЭМЃЈ1ЃЉЁБЃЌЪдЬНОПЁЯBDCгыЁЯAЁЂЁЯBЁЂЁЯCжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЧыФужБНгРћгУвдЩЯНсТлЃЌНтОівдЯТЮЪЬтЃК
ЂйШчЭМЃЈ2ЃЉЃЌАбвЛПщШ§НЧГпXYZЗХжУдкЁїABCЩЯЪЙШ§НЧГпЕФСНЬѕжБНЧБпXYЁЂXZЧЁКУОЙ§ЕуBЁЂCЃЌШєЁЯAЃН40ЁуЃЌдђЁЯABX+ЁЯACXЃНЁЁ ЁЁЁуЃЎ
ЂкШчЭМЃЈ3ЃЉЃЌDCЦНЗжЁЯADBЃЌECЦНЗжЁЯAEBЃЌШєЁЯDAEЃН40ЁуЃЌЁЯDBEЃН130ЁуЃЌЧѓЁЯDCEЕФЖШЪ§ЃЎ

ЁОД№АИЁПЃЈ1ЃЉЁЯBDCЃНЁЯBAC+ЁЯB+ЁЯCЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉЂй50ЃЛЂкЁЯDCEЃН85ЁуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШСЌНгADВЂбгГЄжСЕуFЃЌШЛКѓИљОнЭтНЧЕФаджЪЃЌМДПЩХаЖЯГіЁЯBDCЃНЁЯBAC+ЁЯB+ЁЯCЃЛ
ЃЈ2ЃЉЂйгЩЃЈ1ЃЉПЩЕУЁЯA+ЁЯABX+ЁЯACXЃНЁЯXЃЌШЛКѓИљОнЁЯAЃН40ЁуЃЌЁЯXЃН90ЁуЃЌМДПЩЧѓНтЃЛ
ЃЈ3ЃЉЂкгЩЁЯAЃН40ЁуЃЌЁЯDBEЃН130ЁуЃЌЧѓГіЁЯADE+ЁЯAEBЕФжЕЃЌШЛКѓИљОнЁЯDCEЃНЁЯA+ЁЯADC+ЁЯAECЃЌЧѓГіЁЯDCEЕФЖШЪ§МДПЩ.
ЃЈ1ЃЉШчЭМЃЌЁЯBDCЃНЁЯBAC+ЁЯB+ЁЯCЃЌРэгЩЪЧЃК
Й§ЕуAЁЂDзїЩфЯпAFЃЌ
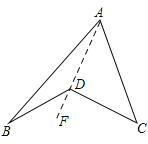
ЁпЁЯFDCЃНЁЯDAC+ЁЯCЃЌЁЯBDFЃНЁЯB+ЁЯBADЃЌ
ЁрЁЯFDC+ЁЯBDFЃНЁЯDAC+ЁЯBAD+ЁЯC+ЁЯBЃЌ
МДЁЯBDCЃНЁЯBAC+ЁЯB+ЁЯCЃЛ
ЃЈ2ЃЉЂйШчЭМЃЈ2ЃЉЃЌЁпЁЯXЃН90ЁуЃЌ
гЩЃЈ1ЃЉжЊЃКЁЯA+ЁЯABX+ЁЯACXЃНЁЯXЃН90ЁуЃЌ
ЁпЁЯAЃН40ЁуЃЌ
ЁрЁЯABX+ЁЯACXЃН50ЁуЃЌ
ЙЪД№АИЮЊЃК50ЃЛ
ЂкШчЭМЃЈ3ЃЉЃЌЁпЁЯAЃН40ЁуЃЌЁЯDBEЃН130ЁуЃЌ
ЁрЁЯADE+ЁЯAEBЃН130ЁуЉ40ЁуЃН90ЁуЃЌ
ЁпDCЦНЗжЁЯADBЃЌECЦНЗжЁЯAEBЃЌ
ЁрЁЯADCЃН![]() ЁЯADBЃЌЁЯAECЃН
ЁЯADBЃЌЁЯAECЃН![]() ЁЯAEBЃЌ
ЁЯAEBЃЌ
ЁрЁЯADC+ЁЯAECЃН![]() ЃН45ЁуЃЌ
ЃН45ЁуЃЌ
ЁрЁЯDCEЃНЁЯA+ЁЯADC+ЁЯAECЃН40Ёу+45ЁуЃН85ЁуЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЎдк
ЃЎдк![]() БпЩЯга
БпЩЯга![]() ИіВЛЭЌЕФЕу
ИіВЛЭЌЕФЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁЇЁЇЁЇЁЇЃЌ
ЃЌЁЇЁЇЁЇЁЇЃЌ![]() ЃЌЙ§ет
ЃЌЙ§ет![]() ИіЕуЗжБ№зї
ИіЕуЗжБ№зї![]() ЕФФкНгОиаЮ
ЕФФкНгОиаЮ![]() ЃЌ
ЃЌ![]() ЃЌЁЇЁЇЁЇЁЇЃЌ
ЃЌЁЇЁЇЁЇЁЇЃЌ![]() ЃЌЩшУПИіОиаЮЕФжмГЄЗжБ№ЮЊ
ЃЌЩшУПИіОиаЮЕФжмГЄЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЁЇЁЇЁЇЁЇЃЌ
ЃЌЁЇЁЇЁЇЁЇЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЁЇЁЇЁЇЁЇ
ЁЇЁЇЁЇЁЇ![]() ________ЃЎ
________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊRtЁїABCжаЃЌЁЯACB=90ЁуЃЎЧыЭъГЩвдЯТШЮЮёЃЎ
ЃЈ1ЃЉГпЙцзїЭМЃКЂйзїЁЯAЕФЦНЗжЯпЃЌНЛCBгкЕуDЃЛ
ЂкЙ§ЕуDзїABЕФДЙЯпЃЌДЙзуЮЊЕуEЃЎЧыБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЌВЂБъУїзжФИЃЎ
ЃЈ2ЃЉШєAC=3ЃЌBC=4ЃЌЧѓCDЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌAC=BCЃЌЕуDдкBCЩЯЃЌзїЁЯADF=ЁЯBЃЌDFНЛЭтНЧЁЯACEЕФЦНЗжЯпCFгкЕуFЃЎ

ЃЈ1ЃЉЧѓжЄЃКCFЁЮABЃЛ
ЃЈ2ЃЉШєЁЯCAD=20ЁуЃЌЧѓЁЯCFDЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуPДг![]() ГіЗЂЃЌбиЫљЪОЗНЯђдЫЖЏЃЌУПЕБХіЕНГЄЗНаЮOABCЕФБпЪБЛсНјааЗДЕЏЃЌЗДЕЏЪБЗДЩфНЧЕШгкШыЩфНЧЃЌЕБЕуPЕк2018ДЮХіЕНГЄЗНаЮЕФБпЪБЃЌЕуPЕФзјБъЮЊ______ЃЎ
ГіЗЂЃЌбиЫљЪОЗНЯђдЫЖЏЃЌУПЕБХіЕНГЄЗНаЮOABCЕФБпЪБЛсНјааЗДЕЏЃЌЗДЕЏЪБЗДЩфНЧЕШгкШыЩфНЧЃЌЕБЕуPЕк2018ДЮХіЕНГЄЗНаЮЕФБпЪБЃЌЕуPЕФзјБъЮЊ______ЃЎ

ЁОД№АИЁП![]()
ЁОНтЮіЁП
ИљОнЗДЩфНЧгыШыЩфНЧЕФЖЈвхзїГіЭМаЮЃЛгЩЭМПЩжЊЃЌУП6ДЮЗДЕЏЮЊвЛИібЛЗзщвРДЮбЛЗЃЌгУ2018Г§вд6ЃЌИљОнЩЬКЭгрЪ§ЕФЧщПіШЗЖЈЫљЖдгІЕФЕуЕФзјБъМДПЩЃЎ
НтЃКШчЭМЫљЪОЃКОЙ§6ДЮЗДЕЏКѓЖЏЕуЛиЕНГіЗЂЕу![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЕБЕуPЕк2018ДЮХіЕНОиаЮЕФБпЪБЮЊЕк337ИібЛЗзщЕФЕк2ДЮЗДЕЏЃЌ
ЕБЕуPЕк2018ДЮХіЕНОиаЮЕФБпЪБЮЊЕк337ИібЛЗзщЕФЕк2ДЮЗДЕЏЃЌ
![]() ЕуPЕФзјБъЮЊ
ЕуPЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ
ЁОЕуОІЁП
ДЫЬтжївЊПМВщСЫЕуЕФзјБъЕФЙцТЩЃЌзїГіЭМаЮЃЌЙлВьГіУП6ДЮЗДЕЏЮЊвЛИібЛЗзщвРДЮбЛЗЪЧНтЬтЕФЙиМќЃЎ
ЁОЬтаЭЁПЬюПеЬт
ЁОНсЪјЁП
15
ЁОЬтФПЁПЮЊСЫБЃЛЄЛЗОГЃЌФГЙЋНЛЙЋЫООіЖЈЙКТђAЁЂBСНжжаЭКХЕФШЋаТЛьКЯЖЏСІЙЋНЛГЕЙВ10СОЃЌЦфжаAжжаЭКХУПСОМлИёЮЊaЭђдЊЃЌУПФъНкЪЁгЭСПЮЊ![]() ЭђЩ§ЃЛBжжаЭКХУПСОМлИёЮЊbЭђдЊЃЌУПФъНкЪЁгЭСПЮЊ
ЭђЩ§ЃЛBжжаЭКХУПСОМлИёЮЊbЭђдЊЃЌУПФъНкЪЁгЭСПЮЊ![]() ЭђЩ§ЃКОЕїВщЃЌЙКТђвЛСОAаЭГЕБШЙКТђвЛСОBаЭГЕЖр20ЭђдЊЃЌЙКТђ2СОAаЭГЕБШЙКТђ3СОBаЭГЕЩй60ЭђдЊЃЎ
ЭђЩ§ЃКОЕїВщЃЌЙКТђвЛСОAаЭГЕБШЙКТђвЛСОBаЭГЕЖр20ЭђдЊЃЌЙКТђ2СОAаЭГЕБШЙКТђ3СОBаЭГЕЩй60ЭђдЊЃЎ
![]() ЧыЧѓГіaКЭbЃЛ
ЧыЧѓГіaКЭbЃЛ
![]() ШєЙКТђетХњЛьКЯЖЏСІЙЋНЛГЕУПФъФмНкЪЁ
ШєЙКТђетХњЛьКЯЖЏСІЙЋНЛГЕУПФъФмНкЪЁ![]() ЭђЩ§ЦћгЭЃЌЧѓЙКТђетХњЛьКЯЖЏСІЙЋНЛГЕашвЊЖрЩйЭђдЊЃП
ЭђЩ§ЦћгЭЃЌЧѓЙКТђетХњЛьКЯЖЏСІЙЋНЛГЕашвЊЖрЩйЭђдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDКЭОиаЮPEFGжаЃЌAB=8ЃЌBC=6ЃЌPE=2ЃЌPG=4ЃЎPEгыACНЛгкЕуMЃЌEFгыACНЛгкЕуNЃЌЖЏЕуPДгЕуAГіЗЂбиABвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШЯђЕуBдШЫйдЫЖЏЃЌАщЫцЕуPЕФдЫЖЏЃЌОиаЮPEFGдкЩфЯпABЩЯЛЌЖЏЃЛЖЏЕуKДгЕуPГіЗЂбиелЯпPEЉЉEFвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШдШЫйдЫЖЏЃЎЕуPЁЂKЭЌЪБПЊЪМдЫЖЏЃЌЕБЕуKЕНДяЕуFЪБЭЃжЙдЫЖЏЃЌЕуPвВЫцжЎЭЃжЙЃЎЩшЕуPЁЂKдЫЖЏЕФЪБМфЪЧtУыЃЈtЃО0ЃЉЃЎ
ЃЈ1ЃЉЕБt=1ЪБЃЌKE=_____ЃЌEN=_____ЃЛ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌЁїAPMЕФУцЛ§гыЁїMNEЕФУцЛ§ЯрЕШЃП
ЃЈ3ЃЉЕБЕуKЕНДяЕуNЪБЃЌЧѓГіtЕФжЕЃЛ
ЃЈ4ЃЉЕБtЮЊКЮжЕЪБЃЌЁїPKBЪЧжБНЧШ§НЧаЮЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAC=15ЃЌBC=8ЃЌDЮЊABЕФжаЕуЃЌEЕудкБпACЩЯЃЌНЋЁїBDEбиDEелЕўЕУЕНЁїB1DEЃЌШєЁїB1DEгыЁїADEжиЕўВПЗжУцЛ§ЮЊЁїADEУцЛ§ЕФвЛАыЃЌдђCE=_____________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЙњЙХДњЪ§бЇЕФаэЖрЗЂЯжЖМдјЮЛОгЪРНчЧАСаЃЌЦфжаЁАбюЛдШ§НЧЁБ(ШчЭМЫљЪО)ОЭЪЧвЛР§.

етИіШ§НЧаЮЕФЙЙдьЗЈдђЮЊЃКСНбќЩЯЕФЪ§ЖМЪЧ1ЃЌЦфгрУПИіЪ§ОљЮЊЦфЩЯЗНзѓгвСНЪ§жЎКЭ.ЪТЪЕЩЯЃЌетИіШ§НЧаЮИјГіСЫ![]() (
(![]() ЮЊе§ећЪ§)ЕФеЙПЊЪН(АД
ЮЊе§ећЪ§)ЕФеЙПЊЪН(АД![]() ЕФДЮЪ§гЩДѓЕНаЁЕФЫГађХХСа)ЕФЯЕЪ§ЙцТЩ.Р§ШчЃЌдкШ§НЧаЮжаЕкШ§ааЕФШ§ИіЪ§1ЁЂ
ЕФДЮЪ§гЩДѓЕНаЁЕФЫГађХХСа)ЕФЯЕЪ§ЙцТЩ.Р§ШчЃЌдкШ§НЧаЮжаЕкШ§ааЕФШ§ИіЪ§1ЁЂ![]() ЁЂ1ЃЌЧЁКУЖдгІ
ЁЂ1ЃЌЧЁКУЖдгІ![]() еЙПЊЪНжаИїЯюЕФЯЕЪ§ЃЛЕкЫФааЕФЫФИіЪ§1ЁЂ
еЙПЊЪНжаИїЯюЕФЯЕЪ§ЃЛЕкЫФааЕФЫФИіЪ§1ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ1ЃЌЧЁКУЖдгІзХ
ЁЂ1ЃЌЧЁКУЖдгІзХ![]() еЙПЊЪНжаИїЯюЕФЯЕЪ§ЕШЕШ.ИљОнЩЯУцЕФЙцТЩЃЌ
еЙПЊЪНжаИїЯюЕФЯЕЪ§ЕШЕШ.ИљОнЩЯУцЕФЙцТЩЃЌ![]() ЕФеЙПЊЪНжаИїЯюЯЕЪ§зюДѓЕФЪ§ЮЊ_______ЃЛЪНзг
ЕФеЙПЊЪНжаИїЯюЯЕЪ§зюДѓЕФЪ§ЮЊ_______ЃЛЪНзг![]()
![]() ЕФжЕЮЊ______.
ЕФжЕЮЊ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБНЧШ§НЧаЮABCжаЃЌЁЯACBЃН90ЁуЃЌЁЯBЃН36ЁуЃЌDЪЧABЕФжаЕуЃЌEDЁЭABНЛBCгкEЃЌСЌНгCDЃЌдђЁЯCDEЃКЁЯECDЃН_____ЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com