
【题目】如图1,在△ABC中,AB=AC,∠BAC=90°,D为AC边上一动点,且不与点A点C重合,连接BD并延长,在BD延长线上取一点E,使AE=AB,连接CE.
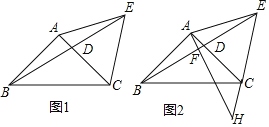
(1)若∠AED=20°,则∠DEC= 度;
(2)若∠AED=a,试探索∠AED与∠AEC有怎样的数量关系?并证明你的猜想;
(3)如图2,过点A作AF⊥BE于点F,AF的延长线与EC的延长线交于点H,求证:EH2+CH2=2AE2.
【答案】(1)45度;(2)∠AEC﹣∠AED=45°,理由见解析;(3)见解析
【解析】
(1)由等腰三角形的性质可求∠BAE=140°,可得∠CAE=50°,由等腰三角形的性质可得∠AEC=∠ACE=65°,即可求解;
(2)由等腰三角形的性质可求∠BAE=180°﹣2α,可得∠CAE=90°﹣2α,由等腰三角形的性质可得∠AEC=∠ACE=45°+α,可得结论;
(3)如图,过点C作CG⊥AH于G,由等腰直角三角形的性质可得EH=![]() EF,CH=
EF,CH=![]() CG,由“AAS”可证△AFB≌△CGA,可得AF=CG,由勾股定理可得结论.
CG,由“AAS”可证△AFB≌△CGA,可得AF=CG,由勾股定理可得结论.
解:(1)∵AB=AC,AE=AB,
∴AB=AC=AE,
∴∠ABE=∠AEB,∠ACE=∠AEC,
∵∠AED=20°,
∴∠ABE=∠AED=20°,
∴∠BAE=140°,且∠BAC=90°
∴∠CAE=50°,
∵∠CAE+∠ACE+∠AEC=180°,且∠ACE=∠AEC,
∴∠AEC=∠ACE=65°,
∴∠DEC=∠AEC﹣∠AED=45°,
故答案为:45;
(2)猜想:∠AEC﹣∠AED=45°,
理由如下:∵∠AED=∠ABE=α,
∴∠BAE=180°﹣2α,
∴∠CAE=∠BAE﹣∠BAC=90°﹣2α,
∵∠CAE+∠ACE+∠AEC=180°,且∠ACE=∠AEC,
∴∠AEC=45°+α,
∴∠AEC﹣∠AED=45°;
(3)如图,过点C作CG⊥AH于G,

∵∠AEC﹣∠AED=45°,
∴∠FEH=45°,
∵AH⊥BE,
∴∠FHE=∠FEH=45°,
∴EF=FH,且∠EFH=90°,
∴EH=![]() EF,
EF,
∵∠FHE=45°,CG⊥FH,
∴∠GCH=∠FHE=45°,
∴GC=GH,
∴CH=![]() CG,
CG,
∵∠BAC=∠CGA=90°,
∴∠BAF+∠CAG=90°,∠CAG+∠ACG=90°,
∴∠BAF=∠ACG,且AB=AC,∠AFB=∠AGC,
∴△AFB≌△CGA(AAS)
∴AF=CG,
∴CH=![]() AF,
AF,
∵在Rt△AEF中,AE2=AF2+EF2,
∴(![]() AF)2+(
AF)2+(![]() EF)2=2AE2,
EF)2=2AE2,
∴EH2+CH2=2AE2.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
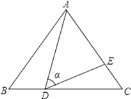
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且 ![]() .下列结论: ①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论: ①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④CD2=CECA.其中正确的结论是________(把你认为正确结论的序号都填上)
;④CD2=CECA.其中正确的结论是________(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
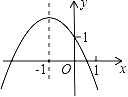
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a﹣b+c>1;③abc>0;④4a﹣2b+c<0;⑤c﹣a>1.其中所有正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
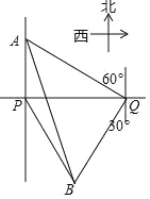
【题目】一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东30°方向,轮船向正东航行了900m,到达Q处,测得A位于北偏西60°方向, B位于南偏西30°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A、B间的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
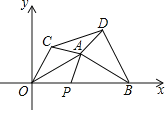
【题目】如图,在平面直角坐标系中,A(![]() ,1),B(2
,1),B(2![]() ,0),点P为线段OB上一动点,将△AOP沿AO翻折得到△AOC,将△ABP沿AB翻折得到△ABD,则△ACD面积的最小值为_____.
,0),点P为线段OB上一动点,将△AOP沿AO翻折得到△AOC,将△ABP沿AB翻折得到△ABD,则△ACD面积的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数![]() 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.
的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
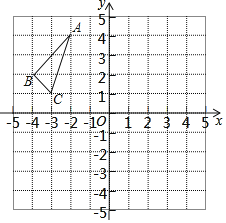
(1)△ABC关于y轴对称图形为△A1B1C1,画出△A1B1C1的图形.
(2)求△ABC的面积.
(3)若P点在x轴上,当BP+CP最小时,直接写出BP+CP最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋里装有2个相同的小球,它们分别写有数字1和2;乙口袋里装有3个相同的小球,它们分别写有数字3,4,5;丙口袋里有2个相同的小球,它们分别写有数字6,7,从三个口袋中各随机地取出1个小球,按要求解答下列问题:
(1)画出“树形图”;
(2)取出的3个小球上只有1个偶数数字的概率是多少?
(3)取出的3个小球上全是奇数数字的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】曲阜限制“三小车辆”出行后,为方便市民出行,准备为![]() 、
、![]() 、
、![]() 、
、![]() 四个村建一个公交车站
四个村建一个公交车站![]() .
.
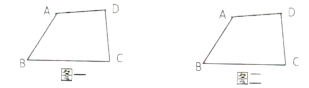
(1)请问:公交站![]() 建在何处才能使它到4个村的距离之和
建在何处才能使它到4个村的距离之和![]() 最小,请在图一中找出点
最小,请在图一中找出点![]() ;
;
(2)请问:公交站![]() 建在何处才能使它到道路
建在何处才能使它到道路![]() 、
、![]() 、
、![]() 的距离相等,请在图二中找出点
的距离相等,请在图二中找出点![]() 并加以说明.
并加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com