
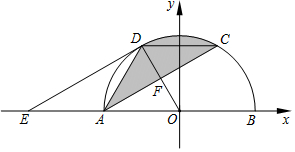
 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交$\widehat{AC}$于点D,过点D作DE∥AC,交BA的延长线于点E,连接AD,CD.
如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交$\widehat{AC}$于点D,过点D作DE∥AC,交BA的延长线于点E,连接AD,CD.分析 (1)连结OC由OA=OC,F为AC的中点,推出OD⊥AC,又DE∥AC,推出OD⊥DE,即可证明DE是⊙O的切线;
(2)①根据S阴=S扇形OCD,计算即可;
②由已知得:$A(-2,0),C(1,\sqrt{3})$推出直线AC的表达式为$y=\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}$,过点P分别作PM⊥x轴,PN⊥AD,垂足分别为M,N,由①得AC平分∠OAD,推出PM=PN,设$P(x,\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3})(-2≤x≤1)$,$PM=PN=\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}$,因为直线DP把阴影部分的面积分成1:2的两部分,分两种情形,讨论即可解决问题.
解答 解:(1)证明:连结OC
∵OA=OC,F为AC的中点,
∴OD⊥AC,
又∵DE∥AC,
∴OD⊥DE,
∴DE是⊙O的切线.
(2)①由(1)得OD⊥DE,
∴∠EDO=90°,
∴OA=AE=2,
∴$AD=\frac{1}{2}OE=2$,
∴OA=OD=AD=2.
∴△AOD是等边三角形,
∴∠AOD=∠DAO=60°,
∴$∠ACD=\frac{1}{2}∠AOD=30°$,
又∵AC⊥OD,
∴∠CAO=∠CAD=30°,
∴∠ACD=∠CAO,
∴CD∥AB,
∴S△ACD=S△OCD,
∴S阴=S扇形OCD,
∵∠CAD=∠OAD-∠OAC=60°-30°=30°,
∴∠COD=2∠CAD=60°,
∴${S_阴}=\frac{{60π×{2^2}}}{360}=\frac{2}{3}π$,
②由已知得:$A(-2,0),C(1,\sqrt{3})$,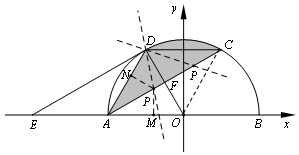
∴直线AC的表达式为$y=\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}$,
过点P分别作PM⊥x轴,PN⊥AD,垂足分别为M,N,
由①得AC平分∠OAD,
∴PM=PN,
设$P(x,\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3})(-2≤x≤1)$,$PM=PN=\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}$,
∵直线DP把阴影部分的面积分成1:2的两部分,
若${S_{△APD}}=\frac{1}{3}{S_阴}$.即$\frac{1}{2}×2•(\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3})=\frac{1}{3}×\frac{2}{3}π$,
解得:$x=\frac{{2\sqrt{3}π-18}}{9}$,此时$P(\frac{{2\sqrt{3}π-18}}{9},\frac{2π}{9})$,
若${S_{△APD}}=\frac{2}{3}{S_阴}$,同理可求得$P(\frac{{4\sqrt{3}π-18}}{9},\frac{4π}{9})$,
综上所述:满足条件的点P的坐标为$P(\frac{{2\sqrt{3}π-18}}{9},\frac{2π}{9})$和$P(\frac{{4\sqrt{3}π-18}}{9},\frac{4π}{9})$.
点评 本题考查圆综合题、一次函数的应用、切线的判定和性质、平行线的性质、扇形的面积公式等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 调查市场上老酸奶的质量情况 | |
| B. | 调查某品牌圆珠笔的使用寿命 | |
| C. | 调查乘坐飞机的旅客是否携带了违禁品 | |
| D. | 调查某市初中生的睡眠情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
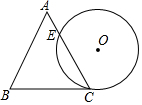 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )| A. | 4cm | B. | 3cm | C. | $\frac{2\sqrt{3}π}{3}$cm | D. | $\frac{\sqrt{3}π}{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(分) | 8.9 | 9.3 | 9.4 | 9.5 | 9.7 | 9.8 |
| 评委(名) | 1 | 2 | 1 | 4 | 1 | 1 |
| A. | 9.3,2 | B. | 9.5,4 | C. | 9.5,9.5 | D. | 9.4,9.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com