练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．若抛物线y=-x2+bx+c经过点（-2，3），则2c-4b-9的值是（　　）
    A．5B．-1C．4D．18

    分析 把（-2，3）代入y=-x2+bx+c可得-2b+c=7，再将所求的式子变形，整体代入即可求出答案

    解答 解：∵抛物线y=-x2+bx+c经过点（-2，3），
    ∴-（-2）2-2b+c=3，
    整理得，-2b+c=7，
    ∴2c-4b-9=2（c-2b）-9=2×7-9=5，
    故选A．

    点评 本题主要考查了二次函数图象上点的坐标特征，利用代入法求得-2b+c=7，再整体代入是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    2．若$\sqrt{x+3}$+（y-2）2=0，则（x+y）2017等于（　　）
    A．-1B．1C．52017D．-52017

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．求下列函数中自变量的取值范围．
    （1）y=2x2+1
    （2）y=$\frac{1}{3-x}$
    （3）y=$\frac{\sqrt{x+1}}{x-1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

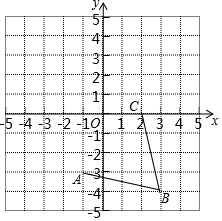    12．如图，在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度，且点A、B、C均在格点上．
    （1）请在所给的网格内画出以线段AB、BC为边的菱形并写出点D的坐标（-2，1）；
    （2）菱形ABCD的周长为4$\sqrt{17}$；
    （3）菱形ABCD的面积为15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，△OAB的OA边在x轴上，其中B点坐标为（3，4）且OB=BA．
    （1）求经过A，B，O三点的抛物线的解析式；
    （2）将（1）中的抛物线沿x轴平移，设点A，B的对应点分别为点A′，B′，若四边形ABB′A′为菱形，求平移后的抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

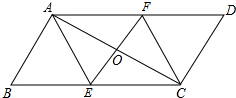    9．如图，点E，F分别放在?ABCD的边BC、AD上，AC、EF交于点O，请你添加一个条件（只添一个即可），使四边形AECF是平行四边形，你所添加的条件是AF=CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，在⊙O中，$\widehat{AC}$=$\widehat{CB}$，CD⊥OA于D，CE⊥OB于E，求证：AD=BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．今有甲、乙、丙三名候选人参与某村村长选举，共发出1800张选票，得票数最高者为当选人，且废票不计入任何一位候选人之得票数内，全村设有四个投开票所，目前第一、第二、第三投开票所已开完所有选票，剩下第四投开票所尚未开票，结果如表所示：
     投开票所 候选人 废票 合计
     甲 乙 丙
     一 200 211 147 12 570
     二 286 85 244 15 630
     三 97 41 205 7 350
     四     250
    （单位：票）
    请回答下列问题：
    （1）请分别写出目前甲、乙、丙三名候选人的得票数；
    （2）承（1），请分别判断甲、乙两名候选人是否还有机会当选村长，并详细解释或完整写出你的解题过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先化简；再求值：（2+x）（2-x）+（-x2y）2，其中x=-1，y=1．

    查看答案和解析>>

    同步练习册答案