
分析 (1)先分解因式,再将除法化成乘法,进行约分;
(2)把-a-1变为-$\frac{a+1}{1}$,再进行通分;
(3)先计算括号里的,再将除法化成乘法,进行约分;
(4)先计算括号里的,再将除法化成乘法,分解因式,最后再约分.
解答 解:(1)$\frac{a-b}{a}÷\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$,
=$\frac{a-b}{a}$•$\frac{a(a-b)}{(a+b)(a-b)}$,
=$\frac{a-b}{a+b}$;
(2)$\frac{{a}^{2}}{a-1}$-a-1,
=$\frac{{a}^{2}}{a-1}$-$\frac{a+1}{1}$,
=$\frac{{a}^{2}-(a+1)(a-1)}{a-1}$,
=$\frac{1}{a-1}$;
(3)$\frac{a-1}{a}÷({a-\frac{1}{a}})$,
=$\frac{a-1}{a}$÷$\frac{{a}^{2}-1}{a}$,
=$\frac{a-1}{a}$•$\frac{a}{(a+1)(a-1)}$,
=$\frac{1}{a+1}$;
(4)(1+$\frac{2}{x-1}$)÷$\frac{x+1}{{x}^{2}-2x+1}$,
=$\frac{x-1+2}{x-1}$•$\frac{(x-1)^{2}}{x+1}$,
=$\frac{x+1}{x-1}$•$\frac{(x-1)^{2}}{x+1}$,
=x-1.
点评 本题考查了分式的混合运算,分解因式是基础;注意运算顺序,有括号的要先计算括号里的,约分前要先分解因式;分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律运算,会简化运算过程.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠B=90°,AB=5,BC=12,AC=13.△ABC内是否有一点P到各边的距离相等?如果有,请作出这一点.说明理由并求出这个距离.
如图,在△ABC中,∠B=90°,AB=5,BC=12,AC=13.△ABC内是否有一点P到各边的距离相等?如果有,请作出这一点.说明理由并求出这个距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25+50x=82.75 | B. | 25(1+x)=82.75 | ||
| C. | 25[1+(1+x)+(1+x)2]=82.75 | D. | 25(1+x)2=82.75 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
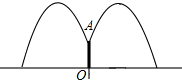 如图,公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,OA=1.5m,水流从A处喷出,在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.若不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?(精确到0.1m)
如图,公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,OA=1.5m,水流从A处喷出,在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.若不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com