
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
(1)求证:△BDF是等边三角形;
(2)连接AF、DC,若BC=3,写出求四边形AFCD面积的思路.
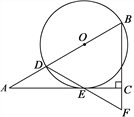
【答案】(1)证明见解析;(2)思路见解析.
【解析】试题分析:(1)连接OE,因AC切⊙O于点E,根据切线的性质可得∠OEA=90° ;再由∠A=30°,∠ACB=90°,根据三角形的内角和定理可得∠AOE=60°,∠B=60°因OD=OE,可得∠ODE=∠OED=60°,所以∠F=∠B=∠ODE,即可判断△BDF是等边三角形 ;(2)如图,作DH⊥AC于点H,求四边形AFCD的面积思路有以下几步:①由∠ACB=90°,∠BAC=30°,BC=3,可求AB,AC的长;②由∠AEO=90°,∠OAE=30°,可知AO=2OE,可求AD,DB,DH的长; ③由(1)可知BF=BD,可求CF的长; ④由AC,DH,CF的长可求四边形AFCD的面积.
试题解析:
(1)证明:连接OE.
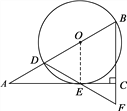
∵AC切⊙O于点E,
∴![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴△BDF是等边三角形.
(2)如图,作DH⊥AC于点H.
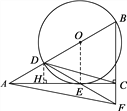
①由∠ACB=90°,∠BAC=30°,BC=3,可求AB,AC的长;
②由∠AEO=90°,∠OAE=30°,可知AO=2OE,可求AD,DB,DH的长;
③由(1)可知BF=BD,可求CF的长;
④由AC,DH,CF的长可求四边形AFCD的面积.


科目:初中数学 来源: 题型:
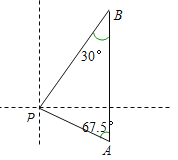
【题目】马航MH370 客机“失联”,我国“海巡01号”前往搜寻。如图某天上午9时,“海巡01号” 轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
证明:DE=BD+CE.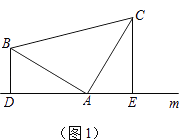
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由. 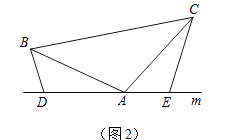
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状. 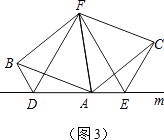
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B坐标分别为A(0,a),B(b,a),且实数a,b满足(a﹣3)2+|b﹣5|=0,现同时将点A,B分别向下平移3个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB. 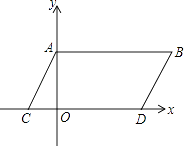
(1)求点C,D的坐标及四边形ABDC的面积;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=S四边形ABDC?若存在这样一点,求出点M的坐标;若不存在,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com