
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 倍
倍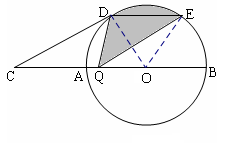
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
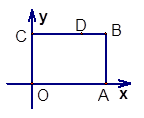
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
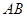 上的点
上的点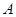 (圆心
(圆心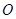 与点
与点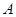 重合)出发,沿直线
重合)出发,沿直线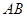 以
以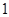 厘米/秒的速度向右运动(圆心
厘米/秒的速度向右运动(圆心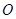 始终在直线
始终在直线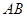 上).已知线段
上).已知线段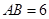 厘米,圆O、圆B的半径分别为
厘米,圆O、圆B的半径分别为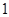 厘米和
厘米和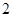 厘米.当两圆相交时,圆O的运动时间
厘米.当两圆相交时,圆O的运动时间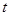 (秒)的取值范围是 .
(秒)的取值范围是 .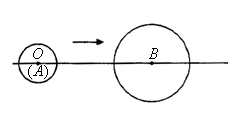
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
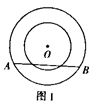
| A.8≤AB≤10 | B.8<AB<10 |
| C.8<AB≤10 | D.6≤AB≤10 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
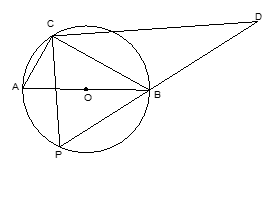
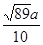 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
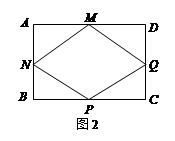

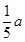 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由; 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com