
 等腰△ABC中,AB=AC,D为底边BC的中点,E为底边上一动点,过E分别向AB,AC作垂线段垂足F,G.连DF,DG.证明:DF=DG,∠EFD=∠EGD,∠FDG=∠FEG=180°-∠A.
等腰△ABC中,AB=AC,D为底边BC的中点,E为底边上一动点,过E分别向AB,AC作垂线段垂足F,G.连DF,DG.证明:DF=DG,∠EFD=∠EGD,∠FDG=∠FEG=180°-∠A. 分析 ①作辅助线,构建垂线段,证明四边形EFMN是矩形和四边形HDPG是矩形,得EN=FM,DH=GP,再证明
△END≌△DHE,则EN=DH,所以FM=GP,根据角平分线性质和等腰三角形三线合一得:DM=DP,所以
△FMD≌△GPD,则DF=DG;
②根据三角形全等和平行线性质得结论;
③利用四边形内角和为360°和垂直定义得:∠BAC+∠FEG=180°,变形后可得结论.
解答 证明:①过D作DM⊥AB于M,作DP⊥AC于P,过E作EN⊥DM于N,过D作DH⊥EG于H,
∵EF⊥AB,
∴∠EFM=∠FMN=∠MNE=90°,
∴四边形EFMN是矩形,
∴EN=FM,
同理得:四边形HDPG是矩形,
∴DH=PG,
∵EN∥AB,DH∥AC,
∴∠NED=∠B,∠HDE=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠NED=∠HDE,
∵∠END=∠EHD=90°,ED=DE,
∴△END≌△DHE,
∴EN=DH,
∴FM=PG,
连接AD,
∵AB=AC,D是BC的中点,
∴AD平分∠BAC,
∴DM=DP,
∴∠FMD=∠DPG=90°,
∴△FMD≌△GPD,
∴DF=DG;
②∵△FMD≌△GPD,
∴∠FDM=∠GDP,
∵EF∥DM,DP∥EG,
∴∠EFD=∠FDM,∠GDP=∠EGD,
∴∠EFD=∠EGD;
③设DF与EG交于点O,
∵∠EFD=∠EGD,∠FOE=∠DOG,
∴∠FEG=∠FDG,
∵EF⊥AB,EG⊥AC,
∴∠AFE=∠AGE=90°,
∴∠BAC+∠FEG=180°,
∴∠FEG=180°-∠BAC,
∴∠FDG=∠FEG=180°-∠BAC.
点评 本题考查了等腰三角形的高线和全等三角形的性质和判定,还考查了角平分线的性质;此题是根据等腰三角形底边上任意一点到两腰的距离和等于腰上的高引申出来的题型,因此本题构建辅助线尤为重要;过底边的中点作两腰的垂线段,构建全等三角形,从而使问题得以解决.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
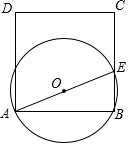 如图,正方形ABCD的边长为1,点E为BC边上一动点,以AE为直径作⊙O.
如图,正方形ABCD的边长为1,点E为BC边上一动点,以AE为直径作⊙O.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y是z的正比例函数 | B. | y是z的反比例函数 | ||
| C. | y是z的函数但不一定是反比例函数 | D. | y是z的函数但不一定是正比例函数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
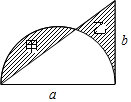 如图,已知直角三角形的两条直角边分别为a、b,以a为直径画一个半圆.若甲、乙两阴影部分的面积相等,则用a的代数式表示b=$\frac{1}{4}$πa.
如图,已知直角三角形的两条直角边分别为a、b,以a为直径画一个半圆.若甲、乙两阴影部分的面积相等,则用a的代数式表示b=$\frac{1}{4}$πa.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com