
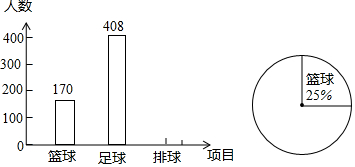
分析 (1)根据题意和统计图中的数据可以求得该校九年级的总人数;
(2)根据(1)中的答案和统计图中的数据可以求出统计图中未知的数据,从而可以将统计图补充完整;
(3)根据统计图中的数据可以估计选择排球类项目的考生约有多少人.
解答  解:(1)由题意可得,
解:(1)由题意可得,
该校九年级共有:170÷25%=680(名)学生,
故答案为:680;
(2)选择排球的人数有:680-170-408=102(人),
选择足球的学生占的百分比为:408÷680×100%=60%,
则选择排球的学生所占的百分比为:1-25%-60%=15%,
故补全的统计图如右图所示;
(3)由题意可得,
2017年全市共有考生21000人,选择排球类项目的考生约有21000×15%=3150(人),
即2017年全市共有考生21000人,选择排球类项目的考生约有3150人.
点评 本题考查条形统计图、扇形统计图、用样本估计总体,解答此类问题的关键是明确题意,利用统计图中的数据求得未知数据.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
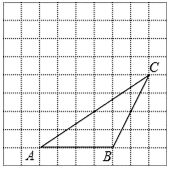 如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的△A′B′C′,再在图中画出△A′B′C′的高C′D′、中线A′E,若S△BCP=S△ACB,P为异于点B的格点,则点P的个数为4个.
如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的△A′B′C′,再在图中画出△A′B′C′的高C′D′、中线A′E,若S△BCP=S△ACB,P为异于点B的格点,则点P的个数为4个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
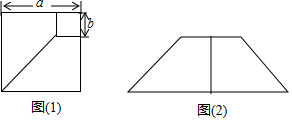
| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | (a+b)2-(a-b)2=4ab |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
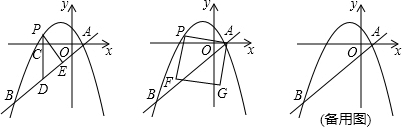
 已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.
已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售量y(百件) | y=-0.1x+8 | y=$\frac{120}{x}$ |
| 销售价格x(元/件) | 30≤x≤60 | 60<x≤80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com