
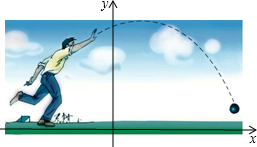
 教练对明明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系满足y=a(x-4)2+h.
教练对明明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系满足y=a(x-4)2+h.分析 (1)利用铅球的最大高度为3m,得出h=3,进一步代入(10,0)求得a,得出函数解析式,令x=0,得出他的出手高度即可;
(2)铅球的最大高度为3.6m,得出h=3.6,进一步代入(0,2)求得a,得出函数解析式,令y=0,得出他的投掷后的落地点距离出手点的水平距离即可;
(3)把点(0,2),(12,0)代入y=a(x-4)2+h得函数解析式,进一步求得最值即可.
解答 解:(1)由题意可知:h=3,
y=a(x-4)2+3,
代入(10,0)解得a=-$\frac{1}{12}$,
则y=-$\frac{1}{12}$(x-4)2+3,
令x=0,则y=$\frac{5}{3}$.
答:他的出手高度是$\frac{5}{3}$m;
(2)由题意可知:y=a(x-4)2+3.6,
代入(0,2)解得a=-$\frac{1}{10}$,
则y=-$\frac{1}{10}$(x-4)2+3.6,
令y=0,解得x=10,
答:他这次投掷后的落地点距离出手点的水平距离是10m;
(3)把(0,2),(12,0)代入y=a(x-4)2+h得
$\left\{\begin{array}{l}{16a+h=2}\\{64a+h=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{24}}\\{h=\frac{8}{3}}\end{array}\right.$,
则y=-$\frac{1}{24}$(x-4)2+$\frac{8}{3}$.
答:铅球行进过程中的最大高度为$\frac{8}{3}$m.
点评 此题考查二次函数的实际运用,掌握待定系数法和顶点式求最值是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A (2$\sqrt{3}$,0)、B(2$\sqrt{3}$,2).将△OAB沿OB折叠后,点A落在点c处,抛物线经过O、A、C三点,其对称轴与OB交于点D.
如图,已知点A (2$\sqrt{3}$,0)、B(2$\sqrt{3}$,2).将△OAB沿OB折叠后,点A落在点c处,抛物线经过O、A、C三点,其对称轴与OB交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知梯形ABCD中,∠A=∠B=90°,AB=AD=12cm,BC=21cm,CD=15cm,E是AD上的点,AE=8cm.
如图,已知梯形ABCD中,∠A=∠B=90°,AB=AD=12cm,BC=21cm,CD=15cm,E是AD上的点,AE=8cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com