
已知:如图, AC∥DF,直线AF分别与直线BD、CE 相交于点G、H,∠1=∠2,
求证: ∠C=∠D.
解:∵∠1=∠2(已知)
∠1=∠DGH( ),
∴∠2=__ _______( 等量代换 )
∴ // ___________( 同位角相等,两直线平行 )
∴∠C=_ _( 两直线平行,同位角相等 )
又∵AC∥DF( )
∴∠D=∠ABG ( )
∴∠C=∠D ( )
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:填空题
如图所示,以O为端点画六条射线后OA,OB,OC,OD,OE,O后F,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2013个点在射线 上.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.
解:∵∠1=∠2(已知),∠2=∠DGF( )
∴∠1=∠DGF
∴BD∥CE( )
∴∠3+∠C=180º( )
又∵∠3=∠4(已知)
∴∠4+∠C=180º
∴ ∥ (同旁内角互补,两直线平行)
∴∠A=∠F( )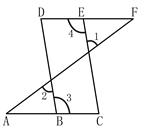
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
一条直线上立有10根距离相等的标杆,一名学生匀速地从第1杆向第10杆行走,当他走到第6杆时用了6.5 s,则当他走到第10杆时所用时间是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
开心画一画(在原图上作图,保留作图痕迹)
【小题1】在AD的右侧作∠DCP=∠DAB;
【小题2】在射线CP上取一点E,使CE=AB,连接BE.AE.
【小题3】画出△ABE的BE边上的高AF和AB边上的高EG.
(2分)如果已知:AB=10,BE=12,EG=6,则AF= (直接填结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com