
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△ABF:S四边形CDEF=2:5;④cos∠CAD=![]() .其中正确的结论有( ).
.其中正确的结论有( ).
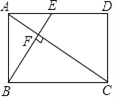
A. 4个 B. 3个 C. 2个 D. 1个
 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】某文具店购进![]() 、
、![]() 两种文具进行销售.若每个
两种文具进行销售.若每个![]() 种文具的进价比每个
种文具的进价比每个![]() 种文具的进价少2元,且用900元正好可以购进50个
种文具的进价少2元,且用900元正好可以购进50个![]() 种文具和50个
种文具和50个![]() 种文具,
种文具,
(1)求每个![]() 种文具和
种文具和![]() 种文具的进价分别为多少元?
种文具的进价分别为多少元?
(2)若该文具店购进![]() 种文具的数量比购进
种文具的数量比购进![]() 种文具的数量的3倍还少5个,购进两种文具的总数量不超过95个,每个
种文具的数量的3倍还少5个,购进两种文具的总数量不超过95个,每个![]() 种文具的销售价格为12元,每个
种文具的销售价格为12元,每个![]() 种文具的销售价格为15元,则将购进的
种文具的销售价格为15元,则将购进的![]() 、
、![]() 两种文具全部售出后,可使总利润超过371元,通过计算求出该文具店购进
两种文具全部售出后,可使总利润超过371元,通过计算求出该文具店购进![]() 、
、![]() 两种文具有哪几种方案?
两种文具有哪几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东家与学校之间是一条笔直的公路,早饭后,小东歩行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回,![]() 时到家,假设小东始终以
时到家,假设小东始终以![]() 的速度步行,两人离家的距离
的速度步行,两人离家的距离![]() (单位:
(单位:![]() )与小东打完电话后的步行时间
)与小东打完电话后的步行时间![]() (单位:
(单位:![]() )之间的函数关系如图所示:
)之间的函数关系如图所示:

(1)小东打电话时,他离家__________![]() .
.
(2)在图中的空格中,填上相应的数据.
(3)小东和妈妈相遇后,妈妈回家的速度为_________![]() .
.
(4)_____________ ![]() 时,两人相距
时,两人相距![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.

(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让学生拓展视野、丰富知识,加深与自然和文化的亲近感,增加对集体生活方式和社会公共道德的体验,我区某中学决定组织部分师生去随州炎帝故里开展研学旅行活动.在参加此次活动的师生中,若每位老师带![]() 个学生,还剩
个学生,还剩![]() 个学生没人带;若每位老师带
个学生没人带;若每位老师带![]() 个学生,就有一位老师少带
个学生,就有一位老师少带![]() 个学生.为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有
个学生.为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有![]() 名老师.现有甲、乙两种大客车,它们的载客量和租金如表所示.
名老师.现有甲、乙两种大客车,它们的载客量和租金如表所示.

(1)参加此次研学旅行活动的老师有 人;学生有 人;租用客车总数为 辆;
(2)设租用![]() 辆乙种客车,租车费用为
辆乙种客车,租车费用为![]() 元,请写出
元,请写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,学校计划此次研学旅行活动的租车总费用不超过![]() 元,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
元,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
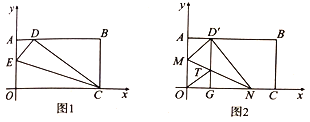
【题目】将一矩形纸片![]() 放在直角坐标系中,
放在直角坐标系中,![]() 为原点,点
为原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() .
.
(1)如图1,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上的
边上的![]() 点处,求直线
点处,求直线![]() 的解析式;
的解析式;
(2)如图2,在![]() 边上选取适当的点
边上选取适当的点![]() ,将
,将![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上的点
边上的点![]() 处,过
处,过![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于
于![]() 点,连接
点,连接![]() ,判断四边形
,判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)、在(2)的条件下,若点![]() 坐标
坐标![]() ,点
,点![]() 在
在![]() 直线上,问坐标轴上是否存在点
直线上,问坐标轴上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形,若存在,请直接写出点
为顶点的四边形是平行四边形,若存在,请直接写出点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备用图甲所示的![]() 型正方形板材和
型正方形板材和![]() 型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
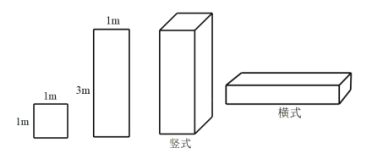
(1)若该工厂准备用不超过2400元的资金去购买![]() ,
,![]() 两种型号板材,制作竖式、横式箱子共10个,已知
两种型号板材,制作竖式、横式箱子共10个,已知![]() 型板材每张20元,
型板材每张20元,![]() 型板材每张60元,问最多可以制作竖式箱子多少只?
型板材每张60元,问最多可以制作竖式箱子多少只?
(2)若该工程新购得65张规格为![]() 型正方形板材,将其全部切割测好难过
型正方形板材,将其全部切割测好难过![]() 型或
型或![]() 型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF过平行四边形ABCD对角线的交点O,交AD于E,交BC于F,若平行四边形ABCD的周长为18,OE=1.5,则四边形EFCD的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料3600kg,乙种原料2410kg,计划利用这两种原料生产A,B两种产品共500件,产品每月均能全部售出.已知生产一件A产品需要甲原料9kg和乙原料3kg;生产一件B种产品需甲种原料4kg和乙种原料8kg.
(1)设生产x件A种产品,写出x应满足的不等式组.
(2)问一共有几种符合要求的生产方案?并列举出来.
(3)若有两种销售定价方案,第一种定价方案可使A产品每件获得利润1.15万元,B产品每件获得利润1.25万元;第二种定价方案可使A和B产品每件都获得利润1.2万元;在上述生产方案中哪种定价方案盈利最多?(请用数据说明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com