
【题目】已知,数轴上有两点A、B对应的数分别为1,5,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A、B的距离相等,求点A、B的距离及x的值.
(2)数轴上是否存在点P,使得点P到点A、B的距离之和最小?若存在,请求出最小值;并求出取得最小值时x可以取的整数值;若不存在,说明理由.
(3)点A、B分别以3个单位长度/秒,2个单位长度/秒的速度向右运动,同时点P以4个单位长度/秒的速度从O点向左运动,当遇到A时,点P立即以不变的速度向右运动,当遇到B时,点P立即以不变的速度向左运动,并不停往返于点A与点B之间,求当点A与点B重合时,点P所经过的总路程是多少?
【答案】(1)1,5,2;(2)存在,最小值为6,x可以取的整数值有1、0、1、2、3、4、5;(3)48
【解析】
(1)根据数轴上的两点距离公式和中点公式列式求解即可;
(2)分类讨论点P分别在点A左侧、点A、点B之间、点B右侧时分别求出,进行比较即可求出最小值;
(3)设经过t分钟点A与点B重合,根据点A比点B运动的距离多6,列出方程,求出t的值,即为点P的运动时间,再乘以点P运动的速度,即可得点P所经过的总路程.
解:(1)∵点A、B对应的数分别为1,5,
∴![]() ,即点A、B的距离为6;
,即点A、B的距离为6;
∵点P到点A、B的距离相等,则P为AB中点,
则有:![]() ,所以
,所以![]() ;
;
(2)数轴上存在点P,使得点P到点A、B的距离之和最小,
当点P在点A左侧时,点P到点A、B的距离之和为:PA+PB=2PA+AB=2PA+6,
当点P在点A、点B之间时,点P到点A、B的距离之和为:PA+PB=AB=6,
当点P在点B右侧时,点P到点A、B的距离之和为:PA+PB=2PB+AB=2PA+6,
所以当点P在点A、点B之间时(含点A、点B),点P到点A、B的距离之和最小,最小值为6,
点A、点B之间的整数值有1、0、1、2、3、4、5,即为x可以取的整数值;
(3)设经过t分钟点A与点B重合,依题意得:
1+3t=5+2t+6,解得:t=12,
所以4t=4×12=48,
所以点P所经过的总路程是48个单位长度.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】某次试验中,测得两个变量v和m的对应数据如下表,则v和m之间的关系最接近下列函数中的( )
m | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
v | ﹣6.10 | ﹣2.90 | ﹣2.01 | ﹣1.51 | ﹣1.19 | ﹣1.05 | ﹣0.86 |
A. v=m2﹣2 B. v=﹣6m C. v=﹣3m﹣1 D. v=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
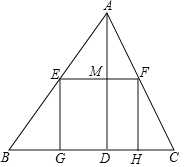
【题目】![]() 是一块锐角三角形材料,边
是一块锐角三角形材料,边![]() ,高
,高![]() ,要把它加工成矩形零件EFHG,使矩形的一边GH在BC上,其余两个顶点E、F在AB、AC上,
,要把它加工成矩形零件EFHG,使矩形的一边GH在BC上,其余两个顶点E、F在AB、AC上,
![]() 求证:EF:
求证:EF:![]() :AD;
:AD;
![]() 设
设![]() ,
,![]() ,用含x的代数式表示y;
,用含x的代数式表示y;
![]() 设矩形EFHG的面积是S,求S与x的函数关系式,并求当x为何值时S取得最大值,最大值为多少?
设矩形EFHG的面积是S,求S与x的函数关系式,并求当x为何值时S取得最大值,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
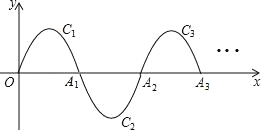
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
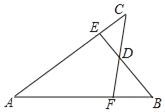
【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
A. ① B. ② C. ①和② D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2x-3,点P在该函数的图象上,点P到x轴、y轴的距离分别为d1、d2.设d=d1+d2,下列结论中: ①d没有最大值; ②d没有最小值; ③ -1<x<3时,d 随x的增大而增大; ④满足d=5的点P有四个.其中正确结论的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表(单位:分):
项目人员 | 阅读能力 | 思维能力 | 表达能力 |
甲 | 93 | 86 | 73 |
乙 | 95 | 81 | 79 |
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将能被录用?
(2)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
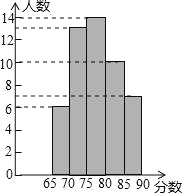
(3)公司按照(2)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数x为:85≤x<90),并决定由高分到低分录用8名员工,甲、乙两人能否被录用?请说明理由,并求出本次招聘人才的录用率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
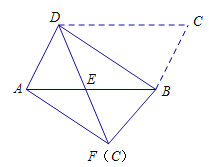
(1)求证:![]() ;
;
(2)判断AF与BD是否平行,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
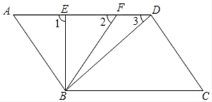
【题目】如图,已知AD∥BC,∠A=∠C=50°,线段AD上从左到右依次有两点E、F(不与A、D重合)
(1)AB与CD是什么位置关系,并说明理由;
(2)观察比较∠1、∠2、∠3的大小,并说明你的结论的正确性;
(3)若∠FBD:∠CBD=1:4,BE平分∠ABF,且∠1=∠BDC,求∠FBD的度数,判断BE与AD是何种位置关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com