
【题目】如图,一次函数y=-![]() x+3
x+3![]() 的图像分别与x轴、y轴交于A、B两点.动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为1,
的图像分别与x轴、y轴交于A、B两点.动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为1,![]() ,2 (长度单位/秒);动点E从O点开始以
,2 (长度单位/秒);动点E从O点开始以![]() (长度单位/秒)的速度沿线段OB运动.设P、E两点同时出发,运动时间为t (秒),当点P沿折线AO-OB-BA运动一周时,动点E和P同时停止运动.过点E作EF∥OA,交AB于点F.
(长度单位/秒)的速度沿线段OB运动.设P、E两点同时出发,运动时间为t (秒),当点P沿折线AO-OB-BA运动一周时,动点E和P同时停止运动.过点E作EF∥OA,交AB于点F.
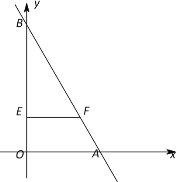
(1)求线段AB的长;
(2)求证:∠ABO=30°;
(3)当t为何值时,点P与点E重合?
(4)当t = 时,PE=PF .
【答案】(1)6;(2)详见解析;(3)![]() ;(4)
;(4)![]()
【解析】
(1)令y=0,求出x,得出A的坐标及OA的长,令x=0,得出B的坐标及OB的长,利用勾股定理即可求出AB的长;
(2)取AB的中点C,连接OC.证明△OAC是等边三角形,得到∠OAB=60°.根据三角形内角和定理即可得出结论;
(3)由于P在OB上与E重合,则E的路程为OE,E所用的时间为t秒,P的路程为OA+OE,P在OA上所用的时间为3秒,在OE上所用的时间为(t-3)秒,根据P在OB上的路程与E的路程相同列方程,求解即可;
(4)先求出点P沿折线AO-OB-BA运动一周时所花的时间为9秒.然后分三种情况讨论:①当P在线段AO上时;②当P在线段OB上时;③当P在线段BA上时.
(1)令y=0,得:y=-![]() x+3
x+3![]() =0,解得:x=3,∴A(3,0),∴OA=3.
=0,解得:x=3,∴A(3,0),∴OA=3.
令x=0,得:y=3![]() ,∴B(0,
,∴B(0,![]() ),∴OB=
),∴OB=![]() .
.
∵∠AOB=90°,∴AB=![]() =6;
=6;
(2)取AB的中点C,连接OC.
∵∠AOB=90°,C为AB的中点,∴OC=BC=CA=3.
∵OA=3,∴OC=CA=OA,∴△OAC是等边三角形,∴∠OAB=60°.
∵∠AOB=90°,∴∠ABO=30°;

(3)由题意得:![]() ,解得:
,解得:![]() ,所以当
,所以当![]() 时,点P与点E重合.
时,点P与点E重合.
(4)P从A到O的时间为t=3÷1=3(秒),P从O到B的时间为![]() ÷
÷![]() =3(秒),P从B到A的时间为:6÷2=3(秒),故点P沿折线AO-OB-BA运动一周时所花的时间为3+3+3=9(秒).分三种情况讨论:
=3(秒),P从B到A的时间为:6÷2=3(秒),故点P沿折线AO-OB-BA运动一周时所花的时间为3+3+3=9(秒).分三种情况讨论:
①当P在线段AO上时,即0<t<3时,由题意知:P(3-t,0),E(0,![]() ).设F(a,b).
).设F(a,b).
∵EF∥OA,∴b=![]() .
.
∵F在直线AB上,∴![]() ,解得:a=
,解得:a=![]() .∴F(
.∴F(![]() ,
,![]() ).
).
∵PE=PF,∴P在EF的垂直平分线上,∴2(3-t)=![]() ,解得:t=
,解得:t=![]() ;
;
②当P在线段OB上时,即3≤t<6时,由题意知:P(0,![]() ),E(0,
),E(0,![]() ),F(
),F(![]() ,
,![]() ).
).
∵PE=PF,∴|![]() -
-![]() |=
|=![]() ,∴
,∴![]() =0,解得:t=9(舍去);
=0,解得:t=9(舍去);
③当P在线段BA上时,即6≤t<9时,由题意知:E(0,![]() ),F(
),F(![]() ,
,![]() ),BP=
),BP= ![]() .设P(m,n),则m=
.设P(m,n),则m=![]() BP=
BP=![]() .
.
∵PE=PF,∴P在EF的垂直平分线上,∴2(t-6)=![]() ,解得:t=
,解得:t=![]() .
.
综上所述:t=![]() 或
或![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图像与x轴交于A(-6,0)与y轴相交于点B,动点P从A出发,沿x轴向x轴的正方向运动.
的图像与x轴交于A(-6,0)与y轴相交于点B,动点P从A出发,沿x轴向x轴的正方向运动.
(1)求b的值,并求出△PAB为等腰三角形时点P的坐标;
(2)在点P出发的同时,动点Q也从点A出发,以每秒![]() 个单位的速度,沿射线AB运动,运动时间为t(s);
个单位的速度,沿射线AB运动,运动时间为t(s);
①点Q的坐标(用含t的表达式表示);
②若点P的运动速度为每秒k个单位,请直接写出当△APQ为等腰三角形时k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= ![]() ,则线段CE的最大值为 .
,则线段CE的最大值为 . 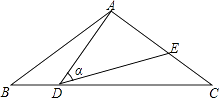
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由一些棱长都为1的小正方体组合成的简单几何体.

![]() 该几何体的表面积
该几何体的表面积![]() 含下底面
含下底面![]() 为______;
为______;
![]() 请画出这个几何体的三视图并用阴影表示出来;
请画出这个几何体的三视图并用阴影表示出来;
![]() 如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体.
如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)若BC=2 ![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为26.6°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O、B、C、A、P在同一平面内,求山坡的坡度.(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin37°≈0.60,tan37°≈0.75)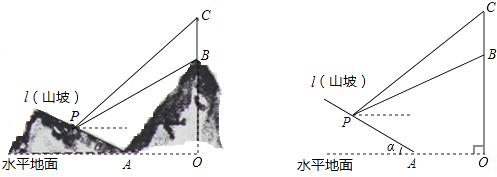
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、②分别是某种型号跑步机的实物图与示意图,已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m). (参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)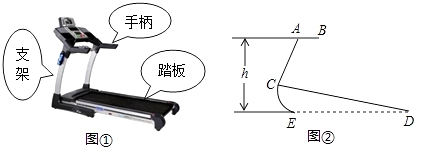
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com