
����Ŀ��Ϊ�˷�������̼���У�2016��10��1�����ij��й������г�����ϵͳ��һ�ڣ������У�Խ��Խ��ľ���ѡ�����г���Ϊ���еĽ�ͨ���ߣ�����ij��ѧ������ȤС��Ϊ���˽�ijС��������з�ʽ�ı仯����������ȡ�˸�С�����־�����е��飬����������ͼ������ͳ��ͼ������ͳ��ͼ��������Ϣδ������

����������ͳ��ͼ������������⣺
��1����������������� ______ �ˣ�
��2���������г�����ϵͳ���к��������ѡ�����г���Ϊ���з�ʽ�İٷֱ�����˶��٣�
��3�������С�����о���2000�ˣ��������г�����ϵͳ���к����ѡ�����г���Ϊ���з�ʽ���ж����ˣ�
���𰸡���1��50����2��20%����3��1000��
�������������������1����������ͼ�����ݼ��㼴�ɣ�
��2������������г����ϵͳ����ǰ����İٷֱȣ����㼴�ɣ�
��3���������������弴�ɣ�
�����������1��������ͼ��֪�����������������10+15+25=50�ˣ�
��2�������г����ϵͳ����ǰ������ѡ�����г���Ϊ���з�ʽ�İٷֱ�Ϊ��15��50=30%��
�������г�����ϵͳ���к���ѡ�����г���Ϊ���з�ʽ�İٷֱ�Ϊ��100%-36%-14%=50%��
50%-30%=20%��
�𣺹������г�����ϵͳ���к��������ѡ�����г���Ϊ���з�ʽ�İٷֱ������20%��
��3���������г�����ϵͳ���к����ѡ�����г���Ϊ���з�ʽ���У�2000��50%=1000�ˣ�


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֵ��
��1��5��3a2b��ab2������ab2+3a2b��������a=��![]() ��b=
��b=![]() ��
��
��2����֪|x+1|+��y��2��2=0����2x2y��2xy2����[��3x2y2+3x2y��+��3x2y2��3xy2��]��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ.
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ.
��1�����A��B�����꼰�����ߵĶԳ�����
��2������B��ֱ��l��y�ύ�ڵ�C����![]() ��ֱ��д��ֱ��l�ı���ʽ��
��ֱ��д��ֱ��l�ı���ʽ��
��3�������![]() �͵�
�͵�![]() �ں���
�ں���![]() ��ͼ���ϣ�PQ=2a��
��ͼ���ϣ�PQ=2a��![]() �� ��
�� ��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ά������Ȩ�棬���齨�Ĺ��Һ���ּӴ������Ϻ���Ѳ�����ȡ�һ�죬�����Һ��ബ�պ�����ij�������������ϵ�A��B����Ѳ�ߣ�ͬʱ����һ�Ҳ��������Ĵ�ֻͣ��C��������ͼ��ʾ��AB��60![]() �����B�����C�ڱ�ƫ��45�ķ����ϣ�A�����C�ڱ�ƫ��30�ķ����ϣ��ں�����AB����һ����D�����AD��120
�����B�����C�ڱ�ƫ��45�ķ����ϣ�A�����C�ڱ�ƫ��30�ķ����ϣ��ں�����AB����һ����D�����AD��120![]() ���
���

��1���ֱ����A��C��B��C�ľ���AC��BC������������ţ�
��2����֪�ڵ���D��Χ100���ﷶΧ���а���Ⱥ������A�����ബ��ACǰ��C���̲飬;����������Σ�գ���������������������������������������������������
���ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��![]() ��2.45��
��2.45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��yΪ�κ�ʵ����x2+y2��4x��2y+8��ֵ���ǣ� ��
A.����
B.����
C.�Ǹ���
D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
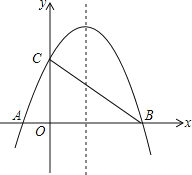
����Ŀ����ͼ����֪������y=��![]() +bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪B�������ΪB��8��0����
+bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪B�������ΪB��8��0����
��1���������ߵĽ���ʽ����Գ��᷽�̣�
��2������AC��BC�����жϡ�AOC���COB�Ƿ����ƣ���˵�����ɣ�
��3��MΪ��������BC֮���һ�㣬NΪ�߶�BC�ϵ�һ�㣬��MN��y�ᣬ��MN�����ֵ��
��4���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��ACQΪ���������Σ������ڣ��������������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
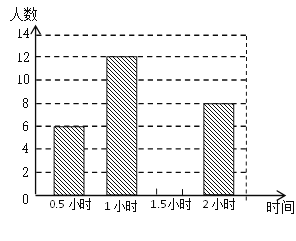
����Ŀ��Ϊ�˹᳹��������Ч���������վ��꼶600��ѧ��ÿ�������ѧϰ�����ijУ�������˾��꼶�IJ���ѧ��������������ÿ������ѧϰ��ʱ�䣮���ݵ�������������������������ͳ��ͼ���£������ͳ��ͼ�е���Ϣ�ش��������⣺
��1���˴γ��������У��������˶�����ѧ����
��2����ͼ21-1����������
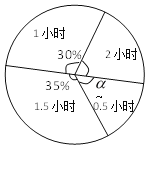
��3�����ͼ21-2��Բ�Ľ�![]() �Ķ�����
�Ķ�����
��4��������У���꼶ѧ������ѧϰʱ�䲻����1.5Сʱ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A(m��3��2)���B(1��n��1)����x��Գƣ���m��________��n��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1�������Σ����ǰ��Ը�������Ϊ�ߵ������γ�Ϊ����������Ρ���ͼ�еġ�ABC���Ǹ�������Σ�������ͼ��ʾ��ƽ��ֱ������ϵ����C������Ϊ��0����1����
��1������ͼ�ķ���ֽ�аѡ�ABC�Ե�OΪλ����������ʹ�Ŵ�ǰ���λ�Ʊ�Ϊ1��2��������A1B1C1����ABC���A1B1C1��λ������O������࣬A��B��C�Ķ�Ӧ��ֱ���A1��B1��C1����
��2�����÷���ֽ�����A1B1C1���Բ��Բ��P��P����������������P�İ뾶=���������������ţ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com