
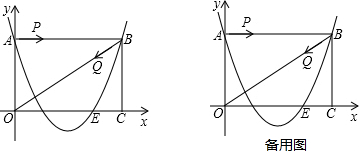
���� ��1�����ݾ��ε����ʼ�OE=OA�ó���A��B��C�����꣬���ô���ϵ�������ɵã�
��2������MΪֱ��AE��Գ���x=2�Ľ���ʱ��ME+MB��ֵ��С������MBE���ܳ���С���ֱ����ֱ��AE�Ľ���ʽ���Ӷ��ó�ֱ��AE��Գ���x=2�Ľ��㼴�ɵã�
��3����BP=BQ��QP=QB��QP=PB��������������������ε����ʵó�����t�ķ��̣����ɵô𰸣�
��� �⣺��1�����ı���OABC�Ǿ��Σ�OA=3��AB=4��
���OAB=��OCB=90�㣬OC=AB=4��CB=OA=3��
�֡�OE=OA=3��
��A�v0��3�w��B�v4��3�w��E�v3��0�w
��������y=ax2+bx+c����A��B��E���㣬
��$\left\{\begin{array}{l}{c=3}\\{9a+3b+c=0}\\{16a+4b+c=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=x2-4x+3��
��2����y=x2-4x+3=��x-2��2-1��
�������ߵĶԳ���Ϊֱ��x=2��
�ߵ�A��B����ֱ��x=2�Գƣ�
��MΪֱ��AE��Գ���x=2�Ľ���ʱ��ME+MB��ֵ��С����BE�ij�һ������ʱ��MBE���ܳ���С��
��ֱ��AE�Ľ���ʽΪy=kx+m��
����$\left\{\begin{array}{l}{m=3}\\{3k+m=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-1}\\{m=3}\end{array}\right.$��
��y=-x+3��
��x=2ʱ��y=1��
��M���������2��1����
��3��������֪PB=4-t��BQ=t��
����BP=BQ����4-t=t��
��ã�t=2��
����QP=QB����ͼ1����QD��AB��D����BD=$\frac{4-t}{2}$��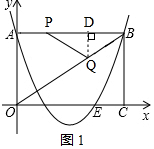
�ߡ�QDB=��OAB=90�㣬��QBD=��OBA��
���QDB�ס�OAB��
��$\frac{BD}{BA}$=$\frac{BQ}{BO}$����$\frac{\frac{4-t}{2}}{4}$=$\frac{t}{5}$��
��ã�t=$\frac{20}{13}$��
����QP=PB����ͼ2����PE��QB��E����BE=$\frac{t}{2}$��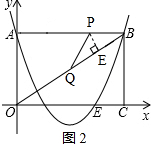
�ߡ�PEB=��OAB=90�㣬��PBE=��OBA��
���PBE�ס�OAB��
��$\frac{PB}{OB}$=$\frac{BE}{BA}$����$\frac{4-t}{5}$=$\frac{\frac{t}{2}}{5}$��
��ã�t=$\frac{32}{13}$��
���ϣ���PBQ�ǵ���������ʱ��t��ֵΪ2��$\frac{20}{13}$��$\frac{32}{13}$��
���� ������Ҫ������κ������ۺ����ã��������վ��ε����ʡ�����ϵ������������ʽ��������߶���̡����������ε��ж������������ε������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
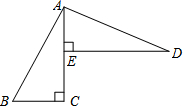 ��֪����ͼ��AC��BC��C��DE��AC��E��AD��AB��A��BC=AE��
��֪����ͼ��AC��BC��C��DE��AC��E��AD��AB��A��BC=AE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 1008 | D�� | 2016 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
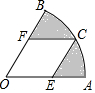 ��ͼ��������OAB�У���O=60�㣬OA=4$\sqrt{3}$���ı���OECF������OAB���������Σ����е�E��C��F�ֱ���OA��$\widehat{AB}$��OB�ϣ���ͼ����Ӱ���ֵ����Ϊ8��-8$\sqrt{3}$��
��ͼ��������OAB�У���O=60�㣬OA=4$\sqrt{3}$���ı���OECF������OAB���������Σ����е�E��C��F�ֱ���OA��$\widehat{AB}$��OB�ϣ���ͼ����Ӱ���ֵ����Ϊ8��-8$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | ���϶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com