
【题目】如图,PA,PB是⊙O的切线,A,B为切点,点C在PB上,OC∥AP,CD⊥AP于点D.
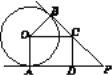
(1)求证:OC=AD;
(2)若∠P=50°,⊙O的半径为4,求四边形AOCD的周长(精确到0.1,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192).
【答案】(1)证明见解析(2)18.4
【解析】
(1)、根据切线的性质得出OA⊥PA,结合已知条件证明出四边形AOCD为矩形,从而得出答案;(2)、根据Rt△OBC中∠BCO的正弦值得出OC的长度,从而得出四边形的周长.
(1)证明:∵PA切⊙O于点A, ∴OA⊥PA,即∠OAD=90°,∵OC∥AP,
∴∠COA=180°-∠OAD=180°-90°=90°, ∵CD⊥AP,∴∠CDA=∠OAD=∠COA=90°,
∴四边形AOCD是矩形,∴OC=AD;
(2)∵PB切⊙O于点B,∴∠OBP=90°, ∵OC∥AP,∴∠BCO=∠P=50°,
在Rt△OBC中,sin∠BCO=![]() ,OB=4, ∴OC=
,OB=4, ∴OC=![]() ≈5.22,
≈5.22,
∴四边形AOCD的周长为2(OA+OC)≈2×(4+5.22)≈18.4.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步,中途改为步行,到达图书馆恰好用时![]() .小东骑自行车以
.小东骑自行车以![]() 的速度直接回家,两人离家的路程
的速度直接回家,两人离家的路程![]() 与各自离开出发地的时间
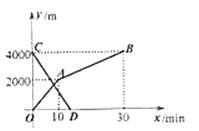
与各自离开出发地的时间![]() 之间的函数图象如图所示,下列说法正确的有几个.( )
之间的函数图象如图所示,下列说法正确的有几个.( )
①家与图书馆之间的路程为![]() ;
;
②小玲步行的速度为![]() ;
;
③两人出发以后8分钟相遇;
④两人出发以后![]() ,
,![]() 、
、![]() 时相距
时相距![]() .
.
A.1B.2
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段MN=3cm,在线段MN上取一点P,使PM=PN;延长线段MN到点A,使AN=![]() MN;延长线段NM到点B,使BN=3BM.
MN;延长线段NM到点B,使BN=3BM.
(1)根据题意,画出图形;
(2)求线段AB的长;
(3)试说明点P是哪些线段的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南开两江中学校初一年级在3月18日听了一堂“树的畅想”的景观设计课,随后在本年级学生中进行了活动收获度调查,采取随机抽样的调查方式进行网络问卷调查,问卷调查的结果分为“非常有收获”“比较有收获”“收获一般”“没有太大的收获”四个等级,分别记作A、B、C、D并根据调查结果绘制两幅不完整统计图:
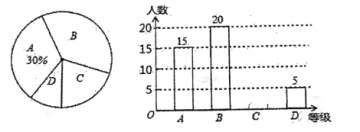
(1)这次一共调查了_______名学生,并将条形统计图补充完整
(2)请在参与调查的这些学生中,随机抽取一名学生,求抽取到的学生对这次“树的畅想”的景观设计课活动收获度是“收获一般”或者“没有太大的收获”的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车一天下午以A地为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:![]() )依次记录如下:+9、-3、-5、+4、-8、+6、-7、-6、-4、+10.
)依次记录如下:+9、-3、-5、+4、-8、+6、-7、-6、-4、+10.
(1)将最后一名乘客送到目的地,出租车离A地多远?在A地的什么地方?
(2)如果出租车每行驶10![]() 所消耗汽油的费用为7元,这天下午共消耗汽油的费用为多少元?
所消耗汽油的费用为7元,这天下午共消耗汽油的费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
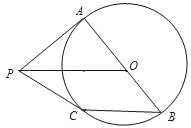
【题目】如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.
(1)判断PC与⊙O的位置关系,并说明理由;
(2)若AB=6,CB=4,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△DEC都是等腰直角三角形,![]() ,
,![]() 连接AE.
连接AE.
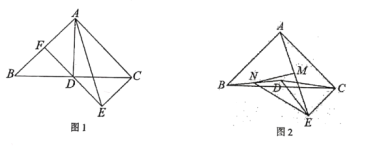
(1)如图(1),点D在BC边上,连接AD,ED延长线交AD于点F,若AB=4,求△ADE的面积
(2)如图2,点D在△ABC的内部,点M是AE的中点,连接BD,点N是BD中点,连接MN,NE,求证![]() 且
且![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背最资料)
低碳生活的理念已逐步被人们所接受,据有关资料统计,一个人平均一年节约的用电相当于减排二氧化碳约18kg;一个人平均一年少买的衣服,相当于减排二氧化碳6kg.
(问题解决)
甲校对本校师生提出“节约用电”的倡议,乙校对本校师生提出“少买衣服”的倡议,2017年两校响应本校倡议的共有1000人,因此而减排二氧化碳总量约13200kg.问:2017年甲、乙两校响应倡议的人数分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com