
 如图,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°且距离A点20海里的C处救生船,此时,遇险船在救生船的正东方向B处,现救生船沿着航线CB前往B处救援,求救生船到达B处行驶的距离?(参考数据:sin68°≈0.90,cos68°≈0.36,tan68°≈2.50,$\sqrt{3}$≈1.7)
如图,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°且距离A点20海里的C处救生船,此时,遇险船在救生船的正东方向B处,现救生船沿着航线CB前往B处救援,求救生船到达B处行驶的距离?(参考数据:sin68°≈0.90,cos68°≈0.36,tan68°≈2.50,$\sqrt{3}$≈1.7) 分析 延长BC交AN于点D,则BC⊥AN于D.先解Rt△ACD,求出CD=$\frac{1}{2}$AC=10,AD=$\sqrt{3}$CD=10$\sqrt{3}$,再解Rt△ABD,得到∠B=22°,AB=$\frac{AD}{sin∠B}$≈46.81,于是得到结论.
解答 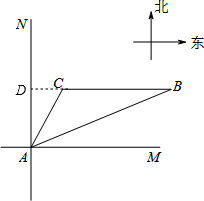 解:如图,延长BC交AN于点D,则BC⊥AN于D.
解:如图,延长BC交AN于点D,则BC⊥AN于D.
在Rt△ACD中,∵∠ADC=90°,∠DAC=30°,
∴CD=$\frac{1}{2}$AC=10,AD=$\sqrt{3}$CD=10$\sqrt{3}$.
在Rt△ABD中,∵∠ADB=90°,∠DAB=68°,
∴∠B=22°,
∴AB=$\frac{AD}{sin∠B}$≈46.81,
BD=AB•cos∠B≈46.81×0.93=43.53,
∴BC=BD-CD=43.53-10=33.53,
答:救生船到达B处行驶的距离是33.53km.
点评 本题考查了解直角三角形的应用-方向角问题,准确作出辅助线构造直角三角形,进而求出BC的长度是解题的关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC边于D,
如图,在△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC边于D,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com