
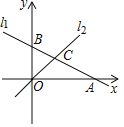
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣2ax+m的图象经过点P(4,5),与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,且S△PAB=10.
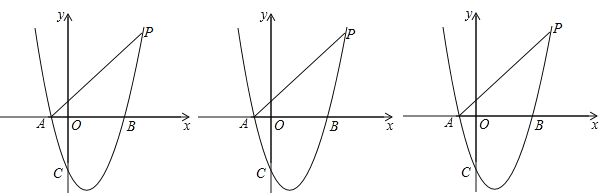
(1)求抛物线的解析式;
(2)在抛物线上是否存在点Q使得△PAQ和△PBQ的面积相等?若存在,求出Q点的坐标,若不存在,请说明理由;
(3)过A、P、C三点的圆与抛物线交于另一点D,求出D点坐标及四边形PACD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
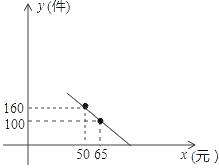
【题目】某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件 40 元,经过记录分析发现,当销售单价在 40 元至 90 元之间(含40 元和 90 元)时,每月的销售量 y(件)与销售单价 x(元)之间的关系可近似地看作一次函数,其图象如图所示.
(1)求 y 与 x 的函数关系式.
(2)设商场老板每月获得的利润为P(元),求 P 与 x 之间的函数关系式;并求出利润的最大时销售单价为多少元?
(3)如果想要每月获得 2400 元的利润,那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
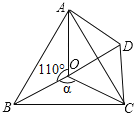
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当△AOD是直角三角形且∠ADO=90°时,求α的度数;
(3)当α=110°或125°或140°时,判断△AOD的形状,请选择其中一种情况说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商品销售某种商品,平均每天可售出20件,每件盈利50元.为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若每件商品降价2元,则平均每天可售出______件;
(2)当每件商品降价多少元时,该商品每天的销售利润为1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
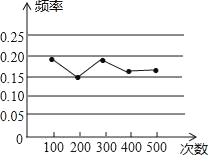
【题目】某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )
A. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
B. 掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6
C. 在“石头剪刀、和”的游戏中,小明随机出的是“剪刀”
D. 袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球
查看答案和解析>>
科目:初中数学 来源: 题型:
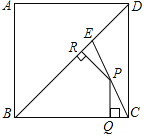
【题目】如图,E为边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任一点,PQ⊥BC于Q,PR⊥BE于R.有下列结论:①△PCQ∽△PER;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论的个数是( )
.其中正确的结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
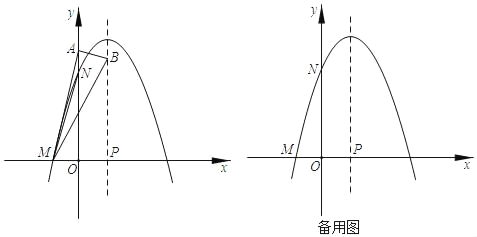
【题目】如图,已知抛物线y=ax2+4x+c与x轴交于点M,与y轴交于点N,抛物线的对称轴与x轴交于点P,OM=1,ON=5.
(1)求抛物线的表达式;
(2)点A是y轴正半轴上一动点,点B是抛物线对称轴上的任意一点,连接AB、AM、BM,且AB⊥AM.
①AO为何值时,△ABM∽△OMN,请说明理由;
②若Rt△ABM中有一边的长等于MP时,请直接写出点A的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com