
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中有一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线。
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线;
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数;
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长。
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长。
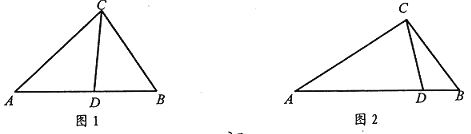
【答案】(1)详见解析;(2)∠ACB=96°或114°;(3)CD=![]() .
.
【解析】
试题分析:(1)由∠A=40°,∠B=60°可得∠ACB=80°,即△ABC不是等腰三角形,再判定△ACD是等腰三角形,△BCD∽△BAC,即可得CD为△ABC的完美分割线;(2)分AD=CD,AD=AC,AC=CD三种情况,根据这三种情况分别求出∠ACB的度数,不合题意的舍去;(3)由△BCD∽△BAC可得![]() ,设BD=x,代入可得
,设BD=x,代入可得![]() ,由于x>0,即可知x=
,由于x>0,即可知x=![]() -1.再由△BCD∽△BAC,所以
-1.再由△BCD∽△BAC,所以![]() ,解得CD=
,解得CD=![]() .
.
试题解析:(1)∵∠A=40°,∠B=60°,
∴∠ACB=80°,
∴△ABC不是等腰三角形,
又因CD为角平分线,
∴∠ACD=∠BCD=![]() ∠ABC=40°,
∠ABC=40°,
∴∠ACD=∠A=40°,
∴△ACD是等腰三角形,
∵∠BCD=∠A=40°,∠B=∠B,
∴△BCD∽△BAC,
∴CD为△ABC的完美分割线;
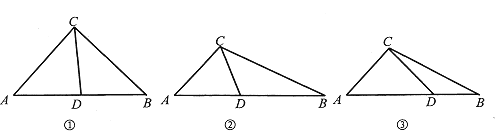
(2)当AD=CD时(如图①),∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°;
当AD=AC时(如图②),∠ACD=∠ADC=![]() ,
,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=114°;
当AC=CD时(如图③),∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∵∠ADC>∠BCD,矛盾,舍去.
∴∠ACB=96°或114°;
(3)由已知AC=AD=2,
∵△BCD∽△BAC,
∴![]() ,
,
设BD=x
∴![]()
解得x=-1±![]() ,
,
∵x>0,
∴x=![]() -1.
-1.
∵△BCD∽△BAC,
∴![]() ,
,
∴CD=![]() .
.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画一条15厘米的线段AB,则AB盖住的整数点的个数共有( )个
A. 13或14个 B. 14或15个 C. 15或16个 D. 16或17个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律,观察下面算式,解答问题.
1+3 =4 =22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
(1)请猜想1+3+5+7+9+…+19=
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n +1)+(2n +3)=
(3)试计算:101 +103+…+197 +199.
查看答案和解析>>
科目:初中数学 来源: 题型:
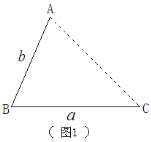
【题目】(1)发现
如图1,点A为线段BC外一动点,且BC=![]() ,AB=
,AB=![]() .
.
填空:当点A位于__________________时,线段AC的长取得最大值,且最大值为_____________.
(用含![]() ,
,![]() 的式子表示)
的式子表示)
(2)应用
点A为线段BC外一动点,且BC=3,AB=1.如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.

(3)拓展
如图3,在平面直角坐标系中,点A的坐标为(2 , 0),点B的坐标为(5 , 0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°.请直接写出线段AM长的最大值及此时点P的坐标.
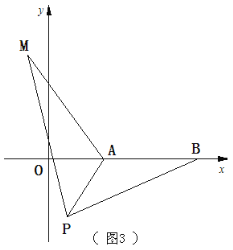
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com