练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
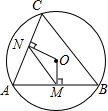
    2．如图，AB、AC都是圆O的弦，OM⊥AB，ON⊥AC垂足分别为M、N，如果MN=6，那么BC=12．

    分析 先根据垂径定理得出M、N分别是AB与AC的中点，故MN是△ABC的中位线，由三角形的中位线定理即可得出结论．

    解答 解：∵OM⊥AB，ON⊥AC垂足分别为M、N，
    ∴M、N分别是AB与AC的中点，
    ∴MN是△ABC的中位线，
    ∴BC=2MN=12．
    故答案为：12．

    点评 本题考查的是垂径定理，熟知平分弦的直径平分这条弦，并且平分弦所对的两条弧是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．如图，△ABC的周长为18cm，BE、CF分别为AC、AB边的中线，BE、CF相交于点O，AO的延长线交BC于D，且AF=3cm，AE=2cm，S△ABC=36cm2．
    （1）求BD的长；
    （2）求S△BOD的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列事件属于必然事件的是（　　）
    A．打开电视，正在播放新闻
    B．实验中学的学生将会有人成为航天员
    C．实数a＜0，则2a＜0
    D．任意买一张电影票，座号是偶数

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，D是△ABC的边AB上一点，已知AC2=AD•AB，求证：∠ACD=∠ABC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．在我市某校的科技活动周中，八年级的7个科技小组交来的科技作品件数分别为：6，5，8，10，8，10，8  这组数据的众数和中位数分别是（　　）
    A．10、6B．10、8C．8、8D．8、6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．（1）计算：（-1）2012-$\sqrt{18}$+2cos45°+|-$\sqrt{4}$|．
    （2）先化简，再求值：（$\frac{1}{x-1}$-$\frac{1}{x+1}$）÷$\frac{x}{{x}^{2}-1}$，其中x=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知：$\frac{2cos60°}{5-2a}$=$\frac{1}{a-1}$，求代数式（1+$\frac{1}{a+1}$）÷$\frac{{a}^{2}+4a+4}{{a}^{2}-1}$的值（先化简，再求值）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在⊙O中，AB=AC，∠A=50°，求∠ABC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知佳莱克服装厂现有A种布料52米，B种布料70米，现计划用这两种布料生产M、N两种型号的时装共80套．已知做一套M型号的时装需用A种布料米0.4，B种布料1.1米，可获利45元；做一套N型号的时装需用A种布料0.9米，B种布料0.6米，可获利50元．设生产M型号的时装套数为x，用这批布料生产两种型号的时装所获得的总利润为y元．
    （1）求y（元）与x（套）的函数关系式，并求出自变量的取值范围；
    （2）当M型号的时装为多少套时，能使该厂所获利润最大？最大利润是多？

    查看答案和解析>>

    同步练习册答案