
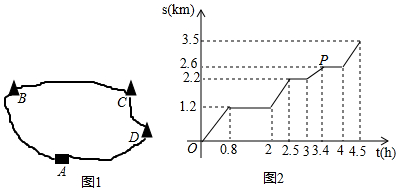
分析 (1)根据图10-2表示甲步行的路程s(km)与游览时间t(h)之间的部分函数图象,即可得到自变量以及因变量;
(2)根据图10-2中第一段水平方向的线段的端点的横坐标,即可得到在景点B处逗留的时间,再根据从景点B到景点C时行走的路程与时间,即可得到速度;
(3)根据函数图象的右端点的纵坐标,即可得到游客沿线路“A→B→C→D→A”共步行的路程;
(4)根据图10-2中点P的横坐标以及纵坐标的实际意义进行判断即可.
解答 解:(1)由题可得,图10-2中自变量是t,因变量是s;
(2)由图可得,该游客在景点B处逗留的时间是1.2小时,他从景点B到景点C时行走的平均速度是$\frac{2.2-1.2}{2.5-2}$=2千米/时;
(3)由图可得,该游客沿线路“A→B→C→D→A”共步行的路程是3.5km;
(4)由题可得,图10-2中点P表示该游客游览3.4小时后步行2.6km.
故答案为:t,s;1.2,2;3.5;该游客游览3.4小时后步行2.6km.
点评 本题考查了一次函数的应用:根据一次函数图象的性质,能从一次函数图象中获取实际问题中的相关数据,同时能用一次函数图象表示实际问题中变化情况.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
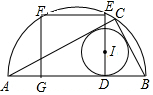 如图,AB为半圆的直径,C是半圆弧上任一点,正方形DEFG的一边DG在直线AB上,另一边DE过△ABC的内切圆圆心I,且点E在半圆弧上,已知DE=9,则△ABC的面积为81.
如图,AB为半圆的直径,C是半圆弧上任一点,正方形DEFG的一边DG在直线AB上,另一边DE过△ABC的内切圆圆心I,且点E在半圆弧上,已知DE=9,则△ABC的面积为81.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
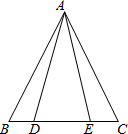 阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.
阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com