
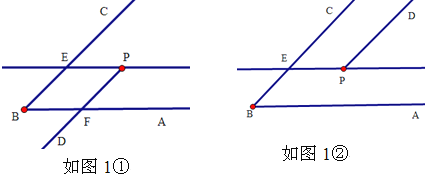
【题目】(1)如图1,P是∠ABC内一点,请过点P画射线PD,使PD∥BC;过点P画直线PE∥BA,交BC于点E.请画图并通过观察思考后你发现∠ABC与∠DPE的大小关系是 ,并说明理由.
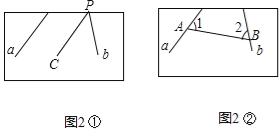
(2)如图2,直线a,b所成的角跑到画板外面去了,为了测量这两条直线所成的角的度数,请画图并简单地写出你的方法.

【答案】(1)相等或互补 (2)见解析
【解析】试题分析:(1)分两种情况讨论;(2)利用平行线的性质或三角形的内角和设计方法.
试题解析:(1)相等或互补
理由如下:
如图1①,
DP交AB于点F.
∵PD∥BC,
∴∠ABC=∠AFP,
∵PE∥BA,
∴∠AFP=∠DPE,
∴∠ABC=∠DPE;
如图1②,
设DP交AB于点F.
∵PD∥BC,
∴∠ABC=∠CEP,
∵PD∥BC,
∴∠CEP+∠DPE=180°,
∴∠ABC+∠DPE=180°;
(2)方法一:
如图2①,设直线b与木板交于点P,
过点P作PC∥a,量出直线b与PC的夹角度数,即为直线a,b所成角的度数,
依据是:两直线平行,同位角相等;
方法二:
如图2②,在直线a,b上各取一点A,B,
连结AB,测得∠1,∠2的度数,
则180°﹣∠1﹣∠2即为直线a,b所成角的度数;
依据是:三角形内角和为180°.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
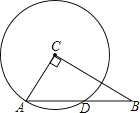
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
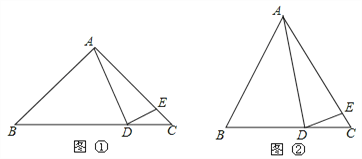
【题目】(14分)探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;
(3)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣a)7÷(﹣a)4×(﹣a)3
(2)a3(﹣b3)2+(﹣2ab2)3
(3)2(a2)3﹣a2![]() a4+(2a4)2÷a2
a4+(2a4)2÷a2
(4)(![]() )﹣3﹣(3.14﹣π)0+(﹣2)4.
)﹣3﹣(3.14﹣π)0+(﹣2)4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
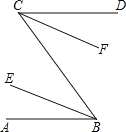
证明:
∵AB∥CD,(已知)
∴∠ =∠ .( )
∵ ,(已知)
∴∠EBC=![]() ∠ABC,(角的平分线定义)
∠ABC,(角的平分线定义)
同理,∠FCB= ![]() ∠BCD .
∠BCD .
∴∠EBC=∠FCB.(等式性质)
∴BE∥CF.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ΔABC和ΔDEF中,已知∠C=∠D,∠B=∠E,要判断这两个三角形全等,还需添加条件( )
A. AB=ED B. AB=FD C. AC=FD D. ∠A =∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将∠AOB绕点O顺时针旋转15°,得到∠COD,若∠COD=45°,则∠AOB的度数是( ).
A.15° B.30° C.45° D.60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com