
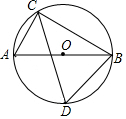
 如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于D.若AC=6,BD=5$\sqrt{2}$,则BC的长为8.
如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于D.若AC=6,BD=5$\sqrt{2}$,则BC的长为8. 分析 连接BD,根据CD是∠ACB的平分线可知∠ACD=∠BCD=45°,故可得出AD=BD,再由AB是⊙O的直径可知△ABD是等腰直角三角形,利用勾股定理求出AB的长,在Rt△ABC中,利用勾股定理可得出BC的长.
解答 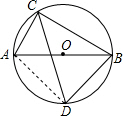 解:连接BD,
解:连接BD,
∵∠ACB=90°,
∴AB是⊙O的直径.
∵ACB的角平分线交⊙O于D,
∴∠ACD=∠BCD=45°,
∴AD=BD=5$\sqrt{2}$.
∵AB是⊙O的直径,
∴△ABD是等腰直角三角形,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{(5\sqrt{2})^{2}+(5\sqrt{2})^{2}}$=10.
∵AC=6,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8.
故答案为:8.
点评 本题考查的是圆周角定理,熟知直径所对的圆周角是直角是解答此题的关键.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知边长为1的小正方形组成的网格中有一个△ABC,点A、B、C均在格点上.
如图,已知边长为1的小正方形组成的网格中有一个△ABC,点A、B、C均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
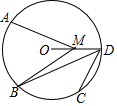 如图,A,B,C,D是⊙O上的四个点,B是$\widehat{AC}$的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )
如图,A,B,C,D是⊙O上的四个点,B是$\widehat{AC}$的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )| A. | 45° | B. | 60° | C. | 75° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 要了解某大洋的海水污染质量情况,宜采用全面调查方式 | |
| B. | 如果有一组数据为5,3,6,4,2,那么它的中位数是6 | |
| C. | 为了解怀化市6月15日到19日的气温变化情况,应制作折线统计图 | |
| D. | “打开电视,正在播放怀化新闻节目”是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-2(x-1)=-3 | B. | 1-2(x-1)=3 | C. | 1-2x-2=-3 | D. | 1-2x+2=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②④ | C. | ①③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com