
ЁОЬтФПЁПФГжжЙЄвЕдСЯЃЌМзВжПтга12ЖжЃЌввВжПтга6ЖжЃЌЯжашДгМзЁЂввСНВжПтНЋетжжЙЄвЕдСЯЗжБ№ЕїЭљAЙЄГЇ10ЖжЃЌBЙЄГЇ8ЖжЃЌвбжЊДгМзВжПтЕїдЫ1ЖждСЯЕНAЃЌBСНЙЄГЇЕФдЫЗбЗжБ№ЪЧ40дЊКЭ80дЊЃЌДгввВжПтЕїдЫ1ЖждСЯЕНAЃЌBСНЙЄГЇЕФдЫЗбЗжБ№ЪЧ30дЊКЭ50дЊЃЎ
ЃЈ1ЃЉШєзмдЫЗбЮЊ900дЊЃЌдђДгМзВжПтЕїдЫЕНAЙЄГЇЕФдСЯЮЊЖрЩйЖжЃП
ЃЈ2ЃЉвЊЪЙзмдЫЗбзюЕЭЃЌгІШчКЮАВХХЕїдЫЗНАИЃП
ЁОД№АИЁПЃЈ1ЃЉМзВжПтЕїдЫЕНAЙЄГЇЕФдСЯЮЊ8ЖжЃЛЃЈ2ЃЉДгМзВжПтЕїдЫЕНAЙЄГЇЕФдСЯЮЊ10ЖжЃЌдђЕїЭљBЙЄГЇЕФдСЯ2ЖжЃЌввВжПтЕїЭљAЙЄГЇдСЯ0ЖжЃЌЕїЭљBЙЄГЇдСЯЮЊ6ЖжЃЌ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшДгМзВжПтЕїдЫЕНAЙЄГЇЕФдСЯЮЊxЖжЃЌдђЕїЭљBЙЄГЇЃЈ12ЉxЃЉЖжЃЌввВжПтЕїЭљAЙЄГЇЃЈ10ЉxЃЉЖжЃЌЕїЭљBЙЄГЇ[6ЉЃЈ10ЉxЃЉ]ЖжЃЌдйИљОнЕїЖЏЕФЪ§СПГЫвдвЛЖжЕФдЫЗбЃЌдйЫуГізмдЫЗбМДПЩЃЛ
ЃЈ2ЃЉИљОнЕїЖЏЕФдСЯЮЊЗЧИКЪ§ПЩЕУ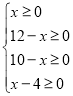 ,дйНтВЛЕШЪНзщПЩЕУxЕФШЁжЕЗЖЮЇЃЌдйЧѓГізюЕЭдЫЗбМДПЩ
,дйНтВЛЕШЪНзщПЩЕУxЕФШЁжЕЗЖЮЇЃЌдйЧѓГізюЕЭдЫЗбМДПЩ
НтЃКЃЈ1ЃЉЩшДгМзВжПтЕїдЫЕНAЙЄГЇЕФдСЯЮЊxЖж
40x+80ЃЈ12ЉxЃЉ+30ЃЈ10ЉxЃЉ+50ЃЈxЉ4ЃЉЃН900
НтЕУЃКxЃН8
Д№ЩшДгМзВжПтЕїдЫЕНAЙЄГЇЕФдСЯЮЊ8Жж
ЃЈ2ЃЉИљОнЕїЖЏЕФдСЯЮЊЗЧИКЪ§ПЩЕУ: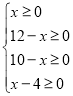 Ёр4ЁмxЁм10
Ёр4ЁмxЁм10
ЩшзмдЫЗбЮЊyдЊЃЌИљОнЬтвтЕУЃКyЃН40x+80ЃЈ12ЉxЃЉ+30ЃЈ10ЉxЃЉ+50ЃЈxЉ4ЃЉЃНЉ20x+1060
ЁпЉ20ЃМ0ЁрyЫцxЕФдіДѓЖјМѕЩй
ЁрЕБxЃН10ЪБЃЌyзюДѓ
МДДгМзВжПтЕїдЫЕНAЙЄГЇЕФдСЯЮЊ10ЖжЃЌдђЕїЭљBЙЄГЇЕФдСЯ2ЖжЃЌввВжПтЕїЭљAЙЄГЇдСЯ0ЖжЃЌЕїЭљBЙЄГЇдСЯЮЊ6Жж.


 ЭЈГЧбЇЕфФЌаДФмЪжЯЕСаД№АИ
ЭЈГЧбЇЕфФЌаДФмЪжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПБпГЄЮЊ4ЕФе§ЗНаЮAOBCдкзјБъЯЕжаЕФЮЛжУШчЭМЫљЪОЃЌШєOBБпБЃГжВЛЖЏЃЌЭЦЖЏAOBCЯђгвЧуаБ30ЁуЕУЫФБпаЮDOBEЃЌдђЕуEЕФзјБъЮЊЃЈЁЁЁЁЃЉ
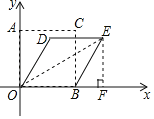
A.ЃЈ5ЃЌ4ЃЉB.ЃЈ6ЃЌ2![]() ЃЉC.ЃЈ6ЃЌ3
ЃЉC.ЃЈ6ЃЌ3![]() ЃЉD.ЃЈ4+2
ЃЉD.ЃЈ4+2![]() ЃЌ5ЃЉ
ЃЌ5ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдк![]() жаЃЌAB=ACЃЌЁЯABC =
жаЃЌAB=ACЃЌЁЯABC =![]() ЃЌDЪЧBCБпЩЯвЛЕуЃЌвдADЮЊБпзї
ЃЌDЪЧBCБпЩЯвЛЕуЃЌвдADЮЊБпзї![]() ЃЌЪЙAE=ADЃЌ
ЃЌЪЙAE=ADЃЌ![]() +
+![]() =180ЁуЃЎ
=180ЁуЃЎ
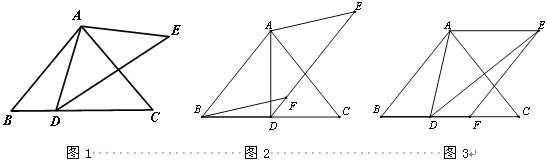
ЃЈ1ЃЉжБНгаДГіЁЯADEЕФЖШЪ§ЃЈгУКЌ![]() ЕФЪНзгБэЪОЃЉЃЛ
ЕФЪНзгБэЪОЃЉЃЛ
ЃЈ2ЃЉвдABЃЌAEЮЊБпзїЦНааЫФБпаЮABFEЃЌ
ЂйШчЭМ2ЃЌШєЕуFЧЁКУТфдкDEЩЯЃЌЧѓжЄЃКBD=CDЃЛ
ЂкШчЭМ3ЃЌШєЕуFЧЁКУТфдкBCЩЯЃЌЧѓжЄЃКBD=CFЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФЖЅЕуCдкxжсЕФИКАыжсЩЯЃЌЕуAдкyжсе§АыжсЩЯЃЌОиаЮOABCЕФУцЛ§ЮЊ8![]() ЃЎАбОиаЮOABCбиDEЗелЃЌЪЙЕуBгыЕуOжиКЯЃЌЕуCТфдкЕкШ§ЯѓЯоЕФGЕуДІЃЌзїEHЁЭxжсгкHЃЌЙ§EЕуЕФЗДБШР§КЏЪ§yЃН
ЃЎАбОиаЮOABCбиDEЗелЃЌЪЙЕуBгыЕуOжиКЯЃЌЕуCТфдкЕкШ§ЯѓЯоЕФGЕуДІЃЌзїEHЁЭxжсгкHЃЌЙ§EЕуЕФЗДБШР§КЏЪ§yЃН![]() ЭМЯѓЧЁКУЙ§DEЕФжаЕуFЃЎдђkЃН_____ЃЌЯпЖЮEHЕФГЄЮЊЃК_____ЃЎ
ЭМЯѓЧЁКУЙ§DEЕФжаЕуFЃЎдђkЃН_____ЃЌЯпЖЮEHЕФГЄЮЊЃК_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
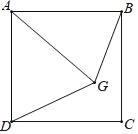
ЁОЬтФПЁПШчЭМЃЌЕуGЮЊе§ЗНаЮABCDФквЛЕуЃЌABЃНAGЃЌЁЯAGBЃН70ЁуЃЌСЊНсDGЃЌФЧУДЁЯBGDЃН_____ЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌADЃН6ЃЌEЮЊABЕФжаЕуЃЌНЋЁїADEбиDEЗелЕУЕНЁїFDEЃЌбгГЄEFНЛBCгкGЃЌFHЁЭBCЃЌДЙзуЮЊHЃЌбгГЄDFНЛBCгыЕуM,СЌНгBFЁЂDGЃЎвдЯТНсТлЃКЂйЁЯBFD+ЁЯADE=180ЁуЃЛЂкЁїBFMЮЊЕШбќШ§НЧаЮЃЛЂлЁїFHBЁзЁїEADЃЛЂмBE=2FMЂнSЁїBFGЃН2.6 ЂоsinЁЯEGBЃН![]() ЃЛЦфжае§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
ЃЛЦфжае§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ

A.3B.4C.5D.6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
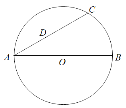
ЁОЬтФПЁПШчЭМЃЌЯпЖЮABЪЧЁбOЕФжБОЖЃЌЕуCдкЁбOЩЯЃЌЧвЁЯCAB=30ЁуЃЌЩшЕуDЪЧЯпЖЮACЩЯШЮвтвЛЕуЃЈВЛКЌЖЫЕуЃЉЃЌСЌНгODЃЌЕБ![]() CD+ODЕФзюаЁжЕЮЊ9ЪБЃЌдђЁбOЕФжБОЖABЕФГЄЮЊ_____ЃЎ
CD+ODЕФзюаЁжЕЮЊ9ЪБЃЌдђЁбOЕФжБОЖABЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁСждкУЛгаСПНЧЦїКЭдВЙцЕФЧщПіЯТЃЌРћгУПЬЖШГпКЭвЛИБШ§НЧАхЛГіСЫвЛИіНЧЕФЦНЗжЯпЃЌЫћЕФзіЗЈЪЧетбљЕФЃКШчЭМЃЌ
ЂйРћгУПЬЖШГпдкЁЯAOBЕФСНБпOAЃЌOBЩЯЗжБ№ШЁOM=ONЃЛ
ЂкРћгУСНИіШ§НЧАхЃЌЗжБ№Й§ЕуMЃЌNЛOMЃЌONЕФДЙЯпЃЌНЛЕуЮЊPЃЛ
ЂлЛЩфЯпOPЃЎдђЩфЯпOPЮЊЁЯAOBЕФЦНЗжЯпЃЎ

ЃЈ1ЃЉЧыаДГіЩфЯпOPЮЊЁЯAOBЕФЦНЗжЯпЕФжЄУїЙ§ГЬЃЎ
ЃЈ2ЃЉЧыИљОнФуЕФжЄУїЙ§ГЬЃЌаДГіаЁСжЕФЛЗЈЕФвРОн______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊвдEЃЈ3ЃЌ0ЃЉЮЊдВаФЃЌвд5ЮЊАыОЖЕФЁбEгыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкCЕуЃЌХзЮяЯп![]() ОЙ§AЃЌBЃЌCШ§ЕуЃЌЖЅЕуЮЊFЃЎ
ОЙ§AЃЌBЃЌCШ§ЕуЃЌЖЅЕуЮЊFЃЎ
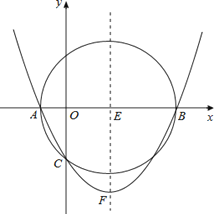
ЃЈ1ЃЉЧѓAЃЌBЃЌCШ§ЕуЕФзјБъЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЖЅЕуFЕФзјБъЃЛ
ЃЈ3ЃЉвбжЊMЮЊХзЮяЯпЩЯвЛЖЏЕуЃЈВЛгыCЕужиКЯЃЉЃЌЪдЬНОПЃК
ЂйЪЙЕУвдAЃЌBЃЌMЮЊЖЅЕуЕФШ§НЧаЮУцЛ§гыЁїABCЕФУцЛ§ЯрЕШЃЌЧѓЫљгаЗћКЯЬѕМўЕФЕуMЕФзјБъЃЛ
ЂкШєЬНОПЂйжаЕФMЕуЮЛгкЕкЫФЯѓЯоЃЌСЌНгMЕугыХзЮяЯпЖЅЕуFЃЌЪдХаЖЯжБЯпMFгыЁбEЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com