
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
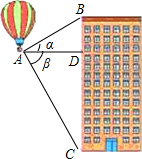 热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?
热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.
在平面直角坐标xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数y=ax2-4ax+2的图象与y轴交于点A,且过点B(3,6).
如图,二次函数y=ax2-4ax+2的图象与y轴交于点A,且过点B(3,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
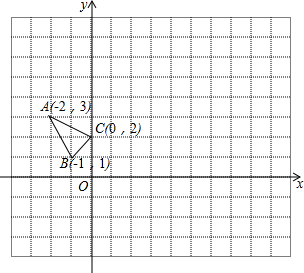
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com