
【题目】如图(1),将两块直角三角尺的直角顶点![]() 叠放在一起,
叠放在一起,
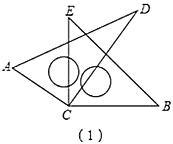
(1)若![]() ,则
,则![]() ______;若
______;若![]() ,则
,则![]() ______;
______;
(2)①猜想![]() 与
与![]() 的大小有何特殊关系,并说明理由;
的大小有何特殊关系,并说明理由;
②应用:当![]() 的余角的4倍等于
的余角的4倍等于![]() 时,则
时,则![]() 是______度
是______度
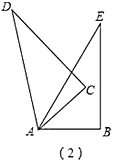
(3)拓展:如图(2),若是两个同样的直角三角尺![]() 锐角的顶点
锐角的顶点![]() 重合在一起,则
重合在一起,则![]() 与
与![]() 的大小又有何关系,直接写出结论不必证明.
的大小又有何关系,直接写出结论不必证明.
【答案】(1)![]() ,
,![]() ;(2)①猜想得
;(2)①猜想得![]() (或
(或![]() 与
与![]() 互补),理由见解析;②30;(3)
互补),理由见解析;②30;(3)![]()
【解析】
(1)本题已知两块直角三角尺实际就是已知三角板的各个角的度数,根据角的和差就可以求出∠ACB,∠DCE的度数;
(2)①根据前两个小问题的结论猜想∠ACB与∠DCE的大小关系,结合前两问的解决思路得出证明;②根据①中的关系式以及![]() 的余角的4倍等于
的余角的4倍等于![]() 列出关于∠DCE的方程,求出∠DCE的度数,最后得出∠BCD的度数即可;
列出关于∠DCE的方程,求出∠DCE的度数,最后得出∠BCD的度数即可;
(3)根据(1)(2)解决思路确定∠DAB与∠CAE的大小并证明.
解:(1)∵∠ECB=90°,∠DCE=35°
∴∠DCB=90°-35°=55°
∵∠ACD=90°,
∴∠ACB=∠ACD+∠DCB=145°.
∵∠ACB=140°,
∴∠DCB=∠ACB-∠ACD=140°-90°=50°.
∴∠DCE=∠ECB-∠DCB=90°-50°=40°,
故答案为:145°,40°
(2)①猜想得∠ACB+∠DCE=180°(或∠ACB与∠DCE互补)
理由:∵∠ECB=90°,∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB-∠DCB=90°-∠DCB
∴∠ACB+∠DCE=180°.
②根据题意得,4(90°-∠DCE)=∠ACB,又由①得,∠ACB=180°-∠DCE,
∴4(90°-∠DCE)=180°-∠DCE,解得∠DCE=60°.
∴∠BCD=90°-∠DCE=30°.
故答案为:30°;
(3)∠DAB+∠CAE=120°.理由如下:
由于∠DAB=∠DAE+∠CAE+∠CAB,
故∠DAB+∠CAE=∠DAE+∠CAE+∠CAB+∠CAE=∠DAC+∠BAE=120°.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.

(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
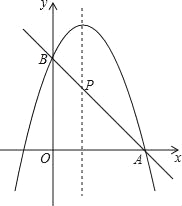
【题目】如图,已知二次函数y=﹣x2+2x+m图象过点A(3,0),与y轴交于点B
(1)求m的值;
(2)若直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分.而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的6位数密码就很有必要了.有一种用“因式分解法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:x3+2x2﹣x﹣2因式分解的结果为(x﹣1)(x+1)(x+2),当x=18时,x﹣1=17,x+1=19,x+2=20,此时可以得到数字密码171920.
(1)根据上述方法,当x=21,y=7时,对于多项式x3﹣xy2分解因式后可以形成哪些数字密码?(写出两个)
(2)若多项式x3+(m﹣3n)x2﹣nx﹣21因式分解后,利用本题的方法,当x=27时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
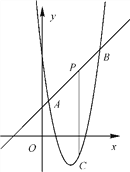
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6相交于A(![]() ,
, ![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴,交抛物线于点C.
(1)求抛物线的表达式;
(2)是否存在这样的点P,使线段PC的长有最大值?若存在,求出这个最大值,若不存在,请说明理由;
(3)当△PAC为直角三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
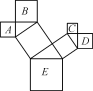
【题目】如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,则最大正方形E的面积是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com