
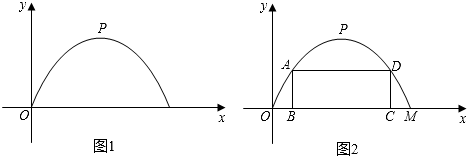
分析 (1)根据题意可以得到抛物线的顶点坐标和抛物线过点(0,0),从而可以求的抛物线的解析式;
(2)根据题意可以用含x的式子表示出AB、AD、DC的长度之和,从而可以解答本题.
解答 解:(1)由题意可得抛物线的顶点坐标为(6,6)且经过原点O(0,0),
设抛物线的解析式为y=a(x-6)2+6,
则0=a(0-6)2+6,解得a=$-\frac{1}{6}$,
即这条抛物线的函数解析式为y=-$\frac{1}{6}(x-6)^{2}+6$(0≤x≤12);
(2)设点A的坐标为(x,$-\frac{1}{6}(x-6)^{2}+6$),则点B的坐标为(x,0),点D的坐标为(12-x,$-\frac{1}{6}(x-6)^{2}+6$),点C的坐标为(12-x,0),
∴AB+AD+DC
=$-\frac{1}{6}(x-6)^{2}+6$+[(12-x)-x]+$-\frac{1}{6}(x-6)^{2}+6$
=$-\frac{1}{3}{x}^{2}+2x+12$
=$-\frac{1}{3}(x-3)^{2}$+15,
∴当x=3时,AB+AD+DC的和取得最大值,此时AB+AD+DC的最大值是15,
即当点A在(3,4.5),点B在(3,0),点D(9,4.5),点C(9,0)时“脚手架”三根木杆AB、AD、DC的长度之和最大,最大值是15.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6天 | B. | 8天 | C. | 10天 | D. | 11天 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 作图并回答问题:
作图并回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
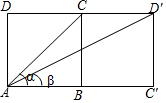 如图,已知正方形ABCD的边长为1,若将边BC绕点B旋转90°后,得到正方形BC′D′C,连接AC、AD′,设∠BAC=α∠C′AD′=β,那么sinα+sinβ等于( )
如图,已知正方形ABCD的边长为1,若将边BC绕点B旋转90°后,得到正方形BC′D′C,连接AC、AD′,设∠BAC=α∠C′AD′=β,那么sinα+sinβ等于( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$+$\sqrt{5}$ | C. | $\frac{{\sqrt{2}+\sqrt{5}}}{10}$ | D. | $\frac{{5\sqrt{2}+2\sqrt{5}}}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com