
【题目】如图,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论正确的有( )

①∠AOC=∠BOD=90°;②∠AOB=20°;③∠AOB=∠AOD-∠AOC;④∠AOB=![]() ∠BOD.
∠BOD.
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
根据已知条件和图形可以得到:∠AOD=∠BOC+2∠COD=110°,则∠AOB=∠COD=20°,由此可以对以下选项通过计算可以做出正确的判定.
解:如图,
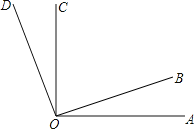
∵∠AOB=∠COD,∠AOD=110°,∠BOC=70°,
∴∠AOD=∠BOC+2∠COD=70°+2∠COD=110°,则∠AOB=∠COD=20°.
①∵∠AOB=∠COD,
∴∠BOC+∠AOB=∠BOC+∠COD=90°,即∠AOC=∠BOD=90°,故①正确;
②∠AOB=∠COD=20°.故②正确;
③由①知,∠AOC=∠BOD=90°,
∴∠AOB=∠AOD-∠BOD=∠AOD-∠AOC,
故③正确;
④∵∠AOB=20°,∠BOD=90°,
∴∠AOB=![]() ∠BOD.
∠BOD.
故④错误.
综上所述,正确的结论有3个.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=kx+b(k≠0)与x轴、y轴分别交于A、B两点,与直线l2:y=3x交于点C,其中点C的坐标为(![]() ,c),点B的坐标为(0,3).
,c),点B的坐标为(0,3).
(1)求点C的坐标;
(2)求直线l1的表达式;
(3)在x轴上有一点D(3,0),求△BCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB于点D,AE⊥BC于点E,AE、CD交于点F,且∠DBF=45°.
(1)若AF=![]() ,BF=
,BF=![]() ,求AB的长;
,求AB的长;
(2)求证:AB﹣CF=![]() BF.
BF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1) 分别写出当0≤x≤100和x>100时,y与x的函数关系式
(2) 利用函数关系式,说明电力公司采取的收费标准
(3) 若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?

查看答案和解析>>
科目:初中数学 来源: 题型:
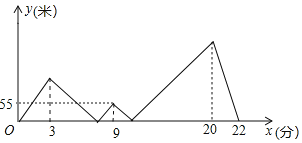
【题目】小明和父亲在一直线公路AB上进行(A→B→A)往返跑训练,两人同时从A点出发,父亲以较快的速度匀速跑到点B休息2分钟后立即原速跑回A点,小明先匀速慢跑了3分钟后,把速度提高到原来的![]() 倍,又经过6分钟后超越了父亲一段距离,小明又将速度降低到出发时的速度,并以这一速度匀速跑到B点看到休息的父亲,然后立即以出发时的速度跑回A点,若两人之间的距离记为y(米),小明的跑步时间记为x(分),y和x的部分函数关系如图所示,则当父亲回到A点时小明距A点______米.
倍,又经过6分钟后超越了父亲一段距离,小明又将速度降低到出发时的速度,并以这一速度匀速跑到B点看到休息的父亲,然后立即以出发时的速度跑回A点,若两人之间的距离记为y(米),小明的跑步时间记为x(分),y和x的部分函数关系如图所示,则当父亲回到A点时小明距A点______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
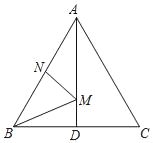
【题目】如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,AD=![]() ,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
A. ![]() B. 2C. 1D. 3
B. 2C. 1D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com